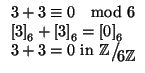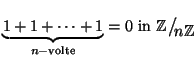

Next: Lezione 12
Up: Matematica Discreta (II modulo)
Previous: Lezione 10
Subsections
Definizione 11.1
Siano
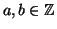
, si dice che
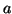
è congruo a
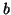
modulo

(in
simboli
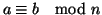
) se
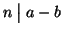
.
Dimostrazione.
1.
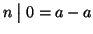 per ogni
per ogni
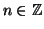 .
.
2. Se
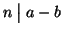 allora
allora 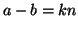 e quindi
e quindi
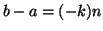 e quindi
e quindi
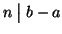 ossia
ossia
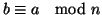 .
.
3. Se
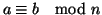 e
e
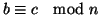 allora
allora
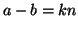 e
e 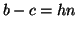 e quindi
e quindi
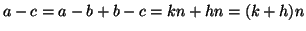 e quindi
e quindi
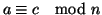 .
.

Ricordiamo la definizione di relazione d'equivalenza su un insieme.
Osservazione 11.4
È prassi comune denotare le relazioni
d'equivalenza con simboli del tipo
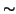
,
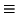
,
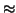
e simili.
Osservazione 11.5
La
proposizione precedente può essere allora rienunciato dicendo che
la
relazione di congruenza modulo  è una relazione d'equivalenza su
è una relazione d'equivalenza su
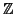
.
Classi d'equivalenza
Definizione 11.6
Siano
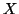
un insieme,
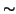
una relazione d'equivalenza su
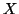
e
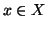
. Si
chiame
classe d'equivalenza di
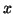
in
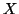
rispetto a
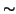
, l'insieme:
Quando non ci sarà ambiguità, si scriverà semplicemente
![$ \left[x\right]$](img949.gif)
invece
che
![$ \left[x\right]_\sim$](img950.gif)
.
L'isieme costituito da tutte le classi d'equivalenza si chiama insieme
quoziente di 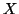 modulo
modulo 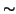 e si denota con il simbolo
e si denota con il simbolo
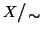 , quindi:
, quindi:
Dimostrazione.
1. Segue dalla proprietà
riflessiva.
2. Se
![$ \left[x\right]=\left[y\right]$](img955.gif) in particolare
in particolare
![$ y\in\left[y\right]=\left[x\right]$](img958.gif) e quindi
e quindi 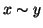 . Viceversa sia
. Viceversa sia
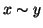 . Se
. Se
![$ z\in \left[x\right]$](img959.gif) allora
allora 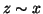 ; per la
proprietà transitiva
; per la
proprietà transitiva 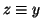 ossia
ossia
![$ z\in\left[y\right]$](img962.gif) , ossia
, ossia
![$ \left[x\right]\subseteq \left[y\right]$](img963.gif) . Scambiando i ruoli di
. Scambiando i ruoli di 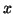 e
e 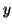 si ha
anche l'inclusione opposta e quindi l'uguaglianza.
si ha
anche l'inclusione opposta e quindi l'uguaglianza.
3. Se
![$ z\in\left[x\right]\cap\left[y\right]$](img965.gif) allora
allora
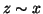 e
e 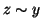 , usando le proprietà
simmetrica e transitiva si ha
allora che
, usando le proprietà
simmetrica e transitiva si ha
allora che 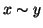 e quindi, per la (2), appena
dimostrata,
e quindi, per la (2), appena
dimostrata,
![$ \left[x\right]=\left[y\right]$](img955.gif) .
.

Osservazione 11.8
Le proprietà (
1) e (
3) assicurano che
l'insieme delle classi d'equivalenza di un insieme rispetto ad una relazione
d'equivalenza (il quoziente) costituisce una
partizione dell'insieme
ossia sono una collezione

di sottinsiemi di
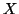
(i.e.
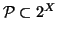
) che hanno
le seguenti proprietà:
- sono tutti non vuoti, ovvero
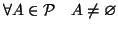 (questo
è garantito da (1))
(questo
è garantito da (1))
- ricoprono
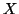 , ovvero
, ovvero
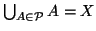 (questo è
garantito da (1))
(questo è
garantito da (1))
- sono a due a due disgiunti, ovvero
 (questo è garantito da (3))
(questo è garantito da (3))
Esercizio 11.1
Sia
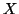
un insieme. Si dimostri che gli insiemi
sono in bigezione.
Soluzione
Definizione 11.9
Siano
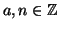
, si chiama classe di congruenza di
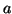
modulo

l'insieme
Indicheremo
![$ \mathbb{Z}\big/\mathchoice
{{}_{\!\displaystyle {}n\mathbb{Z}}}
{{}_{\!\textst...
...riptstyle {}n\mathbb{Z}}}=\big\{\left[a\right]_n\bigm\vert a\in\mathbb{Z}\big\}$](img976.gif)
Osservazione 11.10
Osserviamo che
e quindi
Osservazione 11.11
La classe di congruenza di
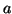
modulo

non è altro che la classe
d'equivalenza di
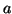
rispetto alla
relazione
d'equivalenza
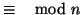
e
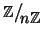
quindi è l'insieme quoziente di
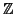
rispetto a
tale relazione d'equivalenza.
In virtù di questa osservazione e della proposizione 11.7 si ha la
seguente:
Dimostrazione.
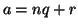 quindi
quindi
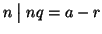 .
.

Corollario 11.14
Se
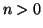
allora
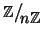
ha esattamente

elementi.
Dimostrazione.
Da 11.13 e dalla 2 di
11.12 segue immediatamente che l'insieme in questione
ha al più  elementi e precisamente
elementi e precisamente
![$ \left[0\right]_n,\left[1\right]_n,\dots,\left[n-1\right]_n$](img988.gif) . D'altra parte se
. D'altra parte se
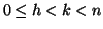 allora
allora 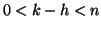 e quindi
e quindi
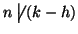 e quindi (sempre
per la 2 di 11.12)
e quindi (sempre
per la 2 di 11.12)
![$ \left[h\right]_n\ne\left[k\right]_m$](img992.gif) .
.

Osservazione 11.15
La proposizione precedente spiega come mai le classi di congruenza modulo

vengono anche chiamate
classi di resto modulo

.
Somma e prodotto di classi di congruenza
Dimostrazione.
(1). Se
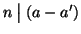 e
e
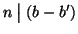 allora
allora
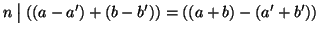 .
.
(2). Esistono
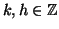 tali che
tali che 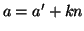 e
e 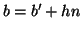 , ma
allora, moltiplicando membro a membro si ottiene
, ma
allora, moltiplicando membro a membro si ottiene
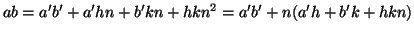 e quindi la tesi.
e quindi la tesi.

Osservazione 11.17
La proposizione precedente permette di definire le operazioni di
somma e prodotto tra classi modulo

. Ponendo
si ottengono delle buone definizioni. Infatti se
![$ \left[a\right]_n=\left[a'\right]_n$](img1009.gif)
e
![$ \left[b\right]_n=\left[b'\right]_n$](img1010.gif)
allora per la
2 di
11.12 si ha che

e
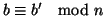
e quindi
per la
proposizione precedente si ha che
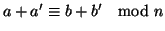
e
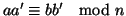
e quindi di nuovo per la
2 di
11.12 si ha che
![$ \left[a+b\right]_n=\left[a'+b'\right]_n$](img1013.gif)
e
![$ \left[ab\right]_n=\left[a'b'\right]_n$](img1014.gif)
.
Nel seguito, quando parleremo di classi di congruenza e di operazioni tra esse,
potrà succedere che, nella notazione, confonderemo la classe con uno dei suoi
rappresentanti. Sarà chiaro dal contesto a cosa ci si starà riferendo. Ad
esempio useremo indifferentemente una delle tre espressioni
per indicare lo stesso concetto.
Osservazione 11.18
L'esercizio precedente, mostra che le operazioni tra classi di congruenza
godono delle stesse proprietà di cui godono le operazioni tra interi.
Attenzione però a due importanti differenze:
- Ci possono essere classi diverse da 0 che moltiplicate tra loro danno
0, ad esempio
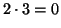
in
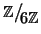
- Se
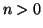 allora
allora


Next: Lezione 12
Up: Matematica Discreta (II modulo)
Previous: Lezione 10
Domenico Luminati
2004-03-18
![]() per ogni
per ogni
![]() .
.
![]() allora
allora ![]() e quindi
e quindi
![]() e quindi
e quindi
![]() ossia
ossia
![]() .
.
![]() e
e
![]() allora
allora
![]() e
e ![]() e quindi
e quindi
![]() e quindi
e quindi
![]() .
.
![]()
![]() modulo
modulo ![]() e si denota con il simbolo
e si denota con il simbolo
![]() , quindi:
, quindi:
![]() in particolare
in particolare
![]() e quindi
e quindi ![]() . Viceversa sia
. Viceversa sia
![]() . Se
. Se
![]() allora
allora ![]() ; per la
proprietà transitiva
; per la
proprietà transitiva ![]() ossia
ossia
![]() , ossia
, ossia
![]() . Scambiando i ruoli di
. Scambiando i ruoli di ![]() e
e ![]() si ha
anche l'inclusione opposta e quindi l'uguaglianza.
si ha
anche l'inclusione opposta e quindi l'uguaglianza.
![]() allora
allora
![]() e
e ![]() , usando le proprietà
simmetrica e transitiva si ha
allora che
, usando le proprietà
simmetrica e transitiva si ha
allora che ![]() e quindi, per la (2), appena
dimostrata,
e quindi, per la (2), appena
dimostrata,
![]() .
.
![]()
![]() quindi
quindi
![]() .
.
![]()
![]() elementi e precisamente
elementi e precisamente
![]() . D'altra parte se
. D'altra parte se
![]() allora
allora ![]() e quindi
e quindi
![]() e quindi (sempre
per la 2 di 11.12)
e quindi (sempre
per la 2 di 11.12)
![]() .
.
![]()
![]() e
e
![]() allora
allora
![]() .
.
![]() tali che
tali che ![]() e
e ![]() , ma
allora, moltiplicando membro a membro si ottiene
, ma
allora, moltiplicando membro a membro si ottiene
![]() e quindi la tesi.
e quindi la tesi.
![]()