In particolare, se
![]() e
e
![]() allora
allora
![]() .
.
Una prima immediata conseguenza del lemma dei cassetti è il seguente corollario:
In particolare, se
![]() e
e
![]() allora
allora
![]() .
.
Questo corollario fa sì che si possa definire la cardinalità degli insiemi finiti.
Dimostrazione.
Se
![]() , allora esiste
, allora esiste
![]() tale che
tale che ![]() è equipotente a
è equipotente a
![]() e
e ![]() è equipotente a
è equipotente a ![]() , ma allora
, ma allora ![]() e
e ![]() sono tra loro
equipotenti (proposizione 2.2. Viceversa se sono equipotenti il
corollario precedente mostra che hanno la stessa cardinalità.
sono tra loro
equipotenti (proposizione 2.2. Viceversa se sono equipotenti il
corollario precedente mostra che hanno la stessa cardinalità.
![]()
Dimostrazione. Procediamo per induzione su
![]() . Se
. Se ![]() allora
allora
![]() e
quindi anche
e
quindi anche
![]() , da cui si conclude. Supponiamo la tesi vera per
, da cui si conclude. Supponiamo la tesi vera per ![]() e
sia dato
e
sia dato ![]() con
con
![]() . Sia
. Sia
![]() una bigezione e poniamo
una bigezione e poniamo
![]() e
e
![]() . Chiaramente
. Chiaramente
![]() è una
bigezione, quindi
è una
bigezione, quindi
![]() . Si hanno due casi
. Si hanno due casi
![]() e
e ![]() . Nel primo caso
. Nel primo caso
![]() , quindi, per ipotesi
di induzione,
, quindi, per ipotesi
di induzione,
![]() . Nel secondo caso, detto
. Nel secondo caso, detto
![]() si ha che
si ha che
![]() e quindi
e quindi
![]() e
quindi
e
quindi
![]() . Si osservi che in
quest'ultimo caso, se
. Si osservi che in
quest'ultimo caso, se ![]() allora anche
allora anche ![]() e quindi, per ipotesi di
induzione si ha che
e quindi, per ipotesi di
induzione si ha che
![]() da cui
da cui
![]() .
.
![]()
Come conseguenza si ha il seguente
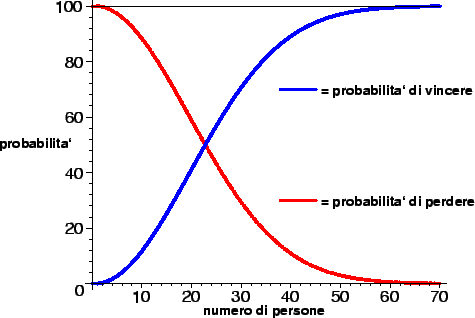
Storiella. Il professore di Matematica Discreta entra nell'aula e davanti ai suoi 60 studenti esclama: --Scommettiamo che due di voi hanno lo stesso compleanno?-- e aggiunge --se io perdo pago la cena a tutti, se vinco voi pagete una cena a me.--
Gli studenti accettano entusiasti la scommessa: --Male che vada ci rimettiamo 50 centesimi ciascuno, ma in ogni caso-- pensano --è praticamente impossibile che il prof. vinca, siamo troppo pochi.--
Una rapida verifica e quindi la delusione: il professore, come ogni anno, si è guadagnato una cena.
Perché il prof. ha vinto? È soltanto una fortuna sfacciata, che gli consente di vincere ogni anno, o è qualcos'altro?
Formalizziamo la situazione. Associare ad ogni studente il proprio giorno di
nascita è una funzione da un insieme ![]() con 60 elementi (l'insieme degli
studenti) in un insieme
con 60 elementi (l'insieme degli
studenti) in un insieme ![]() con 365 elementi (l'insieme dei possibili giorni di
nascita, escludendo il caso degli anni bisestili). Il professore perde se tale
funzione è iniettiva, vince altrimenti. Si tratta allora di contare il numero
di funzioni iniettive, e dividerlo per il numero di funzioni, questo darà la
probabilità di perdere la scommessa da parte del professore.
con 365 elementi (l'insieme dei possibili giorni di
nascita, escludendo il caso degli anni bisestili). Il professore perde se tale
funzione è iniettiva, vince altrimenti. Si tratta allora di contare il numero
di funzioni iniettive, e dividerlo per il numero di funzioni, questo darà la
probabilità di perdere la scommessa da parte del professore.
Questo, assieme al risultato dell'esercizio 4.4 (punto 2), ci
dice che se
![]() e
e
![]() la probabilità che una
funzione
la probabilità che una
funzione ![]() sia iniettiva è pari a
sia iniettiva è pari a
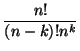
 |