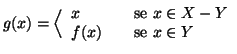

Next: Lezione 6
Up: Matematica Discreta (II modulo)
Previous: Lezione 4
Subsections
Insiemi infiniti: l'assioma della scelta
Uno degli strumenti più potenti di cui si ha spesso bisogno quando si deve
trattare con insiemi infiniti, è il seguente:
Assioma 5.1 (della scelta)
Sia
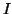
un insieme e per ogni
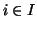
sia dato un insieme
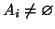
.
Allora esiste una funzione, detta
funzione di scelta,
tale che
Osservazione 5.2
Questo assioma dice essenzialmente che quando si ha un insieme di insiemi non
vuoti è possibile scegliere, in un colpo solo, un elemento da ciascuno
di essi. Si osservi che questo assioma è fortemente non costruttivo:
ci dice che una funzione di scelta esiste, ma non dà alcun modo per
trovarla.
Osservazione 5.3
Una delle situazioni in cui più spesso si adopera l'assioma della scelta (e
che anzi ne è una formulazione equivalente) è la seguente: sia

un
insieme, prendiamo come insieme di indici l'insieme
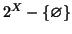
e per
ogni
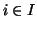
(ossia per ogni
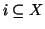
diverso da
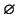
poniamo
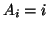
. L'assioma di scelta ci dice allora che esiste una funzione
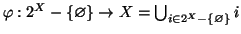
tale che
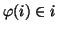
per ogni
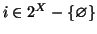
.
Esercizio 5.1
Si provi che una funzione
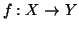
è surgettiva se e solo se esiste
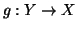
tale che
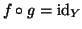
. Una tale
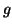
si chiama una
inversa
destra di

.
Soluzione
Esercizio 5.2
Si provi che una funzione
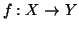
è iniettiva se e solo se esiste
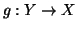
tale che
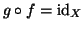
. Una tale
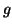
si chiama una
inversa
sinistra di

.
Soluzione
Teorema 5.4
Se

è un insieme infinito, allora contiene un sottinsieme
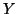
equipotente a
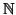
.
Dimostrazione.
Sia
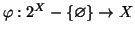 una funzione di scelta e denotiamo con
una funzione di scelta e denotiamo con 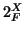 l'insieme delle parti finite di
l'insieme delle parti finite di  , ovvero
, ovvero
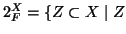 è finito
è finito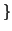 . Dato un elemento
. Dato un elemento
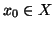 , (che esiste essendo
, (che esiste essendo  infinito e quindi non vuoto) consideriamo la
funzione
infinito e quindi non vuoto) consideriamo la
funzione
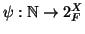 definita ricorsivamente da:
definita ricorsivamente da:
e quindi definiamo la
funzione
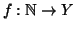 ponendo
ponendo 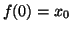 e per ogni
e per ogni 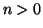 ,
,
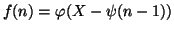 . Osserviamo che, dalla definizione di
. Osserviamo che, dalla definizione di 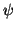 segue che
per ogni
segue che
per ogni
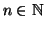 si ha
si ha
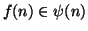 e
e
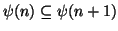 , da
cui segue che se
, da
cui segue che se 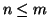 allora
allora
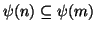 e quindi
e quindi
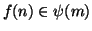 . Ma allora se
. Ma allora se 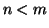 ,
,
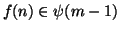 , mentre
, mentre
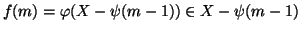 e quindi
e quindi
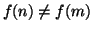 , pertanto
, pertanto  è iniettiva. L'insieme
è iniettiva. L'insieme
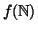 è allora l'insieme cercato.
è allora l'insieme cercato.

Osservazione 5.5
Nella dimostrazione del teorema precedente si definisce ricorsivamente una
funzione
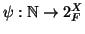
.
La funzione
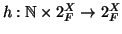
che si in questa definizione ricorsiva
è la funzione data da
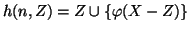
. Si osservi che dato che

è
infinito, se
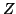
è finito, allora
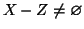
e quindi ha senso prendere
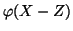
e il risultato dell'applicare
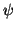
,
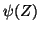
è ancora un insieme
finito. È esattamente in questo punto che si usa l'ipotesi di infinitezza
dell'insieme

.
Osservazione 5.6
In qualche senso il teorema precedente mostra come la cardinalità dei numeri
naturali sia,
in un senso ancora da specificare la ``più piccola'' tra le
cardinalità infinite.
Proposizione 5.7
Ogni insieme infinito è equipotente ad un suo sottinsieme proprio.
Dimostrazione. Sia  un insieme infinito e sia
un insieme infinito e sia
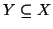 un sottinsieme
equipotente a
un sottinsieme
equipotente a
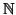 . Abbiamo già visto che
. Abbiamo già visto che
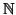 è equipotente ad un suo sottinsieme
proprio, quindi se
è equipotente ad un suo sottinsieme
proprio, quindi se
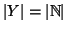 ,
, 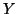 è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione
è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione 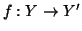 essendo
essendo
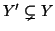 (si provi questa affermazione). Ma allora la funzione
(si provi questa affermazione). Ma allora la funzione
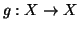 definita da
definita da
dà una bigezione tra  ed il sottinsieme
ed il sottinsieme
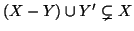 .
.

La proposizione precedente ed il corollario 4.5, provano la
seguente caratterizzazione degli insiemi infiniti.
Teorema 5.8
Un insieme è infinito se e solo se è equipotente ad un suo sottinsieme
proprio.
Esercizio 5.3
Si provi quanto affermato nella dimostrazione della proposizione
5.7, ossia che se
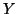
è equipotente a
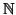
allora
esiste una bigezione di
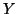
con un suo sottinsieme proprio.
Soluzione


Next: Lezione 6
Up: Matematica Discreta (II modulo)
Previous: Lezione 4
Domenico Luminati
2004-03-18
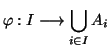
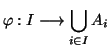
![]() una funzione di scelta e denotiamo con
una funzione di scelta e denotiamo con ![]() l'insieme delle parti finite di
l'insieme delle parti finite di ![]() , ovvero
, ovvero
![]() è finito
è finito![]() . Dato un elemento
. Dato un elemento
![]() , (che esiste essendo
, (che esiste essendo ![]() infinito e quindi non vuoto) consideriamo la
funzione
infinito e quindi non vuoto) consideriamo la
funzione
![]() definita ricorsivamente da:
definita ricorsivamente da:
![]() un insieme infinito e sia
un insieme infinito e sia
![]() un sottinsieme
equipotente a
un sottinsieme
equipotente a
![]() . Abbiamo già visto che
. Abbiamo già visto che
![]() è equipotente ad un suo sottinsieme
proprio, quindi se
è equipotente ad un suo sottinsieme
proprio, quindi se
![]() ,
, ![]() è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione
è equipotente ad un suo
sottinsieme proprio, in parrtcolare esiste una bigezione ![]() essendo
essendo
![]() (si provi questa affermazione). Ma allora la funzione
(si provi questa affermazione). Ma allora la funzione
![]() definita da
definita da