


Next: Lezione 12 (25 marzo
Up: Matematica Discreta
Previous: Lezione 10 (22 marzo
Subsections
Definizione 11.1
Sia
G un gruppo finito si chiama
ordine di
G il numero dei suoi
elementi, e si denota con
o(
G). Se
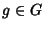
chiamiamo
ordine il numero
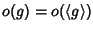
.
Esercizio 11.1
Si provi che
go(g)=1.
Soluzione
Definizione 11.2
Sia
G un gruppo
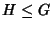
e
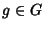
si chiama
classe laterale
sinistra l'insieme
Si chiama
classe laterale destra l'insieme
Siano 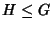 e si consideri la relazione
e si consideri la relazione
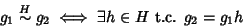 |
(14) |
Osservazione 11.3
Se
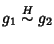
allora
g1=
g2h per qualche
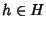
,
e quindi
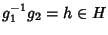
.
Viceversa se
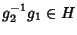
allora
g1-1g2=
hper qualche
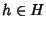
e quindi
g2=
g1h. Ossia
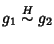
se e solo se
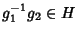
.
Proposizione 11.4
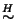
è una relazione d'equivalenza, e per ogni
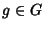
si
ha che
![$\left[g\right]_{\stackrel{H}{\sim}}=gH$](img431.gif)
.
Dim.
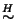 è riflessiva. Dato che H è un
sottogruppo,
è riflessiva. Dato che H è un
sottogruppo, 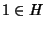 e dato che g=gi si ha che
e dato che g=gi si ha che
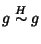 per ogni
per ogni 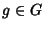 .
.
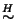 è simmetrica Sia
è simmetrica Sia
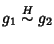 ossia esiste
ossia esiste
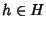 tale che g2=g1 h, ma allora, moltiplicando a destra per
h-1 si ottiene che
g2h-1=g1h h-1=g11=g1 e dato che H è un
sottogruppo
tale che g2=g1 h, ma allora, moltiplicando a destra per
h-1 si ottiene che
g2h-1=g1h h-1=g11=g1 e dato che H è un
sottogruppo
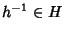 e quindi
e quindi
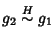 .
.
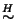 è transitiva. Siano
è transitiva. Siano
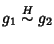 e
e
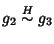 ovvero g2=g1h1 e
g3=g2h2 con
ovvero g2=g1h1 e
g3=g2h2 con
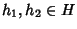 .
Sostituendo la prima
nella seconda si ottiene che
g3=g1h1h2 e dao che H è un
sottogruppo
.
Sostituendo la prima
nella seconda si ottiene che
g3=g1h1h2 e dao che H è un
sottogruppo
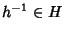 e quindi
e quindi
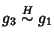 .
.
Che
![$\left[g\right]_{\stackrel{H}{\sim}}=gH$](img431.gif) segue immediatamente dalla definizione di
classe laterale e dalla definizione di classe
d'equivalenza.
segue immediatamente dalla definizione di
classe laterale e dalla definizione di classe
d'equivalenza.

L'insieme quoziente
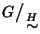 si denota semplicemente
con
si denota semplicemente
con
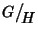 e si chiama il quoziente di G modulo H.
e si chiama il quoziente di G modulo H.
Corollario 11.5
Le classi laterali sinistre gH costituiscono una partizione di G.
Dim.
Segue immediatamente dalla proposizione precedente e dall'analoga
proprietà dimostrata in generale per le classi di una relazione
d'equivalenza qualsiasi (osservazione 7.7).

Lemma 11.6
Sia
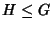
e sia
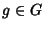
.
Gli insiemi
H e
gH sono in bigezione.
Dim.
Si consideri l'applicazione
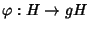 definita da
definita da
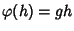 .
L'applicazione è surgettiva per definizione di
classe laterale. Dimostriamo che è anche iniettiva. Se
.
L'applicazione è surgettiva per definizione di
classe laterale. Dimostriamo che è anche iniettiva. Se
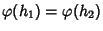 allora gh1=gh2 e quindi, moltiplicando a sinistra
per g-1 si ottiene
allora gh1=gh2 e quindi, moltiplicando a sinistra
per g-1 si ottiene
h1=1h1=g-1gh1=g-1gh2=1h2=h2.

Osservazione 11.7
La proprietà dei gruppi usata nella dimostrazione precedente, ossia che
è nota con il nome di
legge di cancellazione sinistra (l'analoga
ottenuta moltiplicando a destra si chiama
legge di cancellazione
destra). Si osservi che in generale questa non vale nei monoidi, ad esempio
in
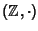
si ha che
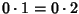
ma
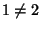
Dim.
Dal lemma precedente segue che le classi laterali di H hano tutte lo stesso
numero di elementi pari ad o(H), quindi, detto k il numero di classi
laterali (ossia il numero di elementi del quoziente
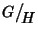 ), dato che
queste sono una partizione, si ha che
o(G)=ko(H) e quindi la tesi.
), dato che
queste sono una partizione, si ha che
o(G)=ko(H) e quindi la tesi.

Definizione 11.9
Un sottogruppo
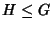
si dice
normale se per ogni
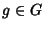
si ha che
gH=
Hg. Per indicare che
H è un sottogruppo normale di
G si
scriverà anche
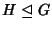
.
Osservazione 11.10
Se
G è commutativo e
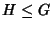
allora dalla
definizione di
classe laterale segue
immediatamente che
gH=
Hg per ogni
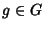
e quindi ogni sottogruppo di un
gruppo commutativo è normale.
Comunque in generale, esistono sottogruppi non normali. Si consideri ad
esempio
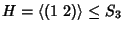
.
Semplici calcoli mostrano che
e quindi
H non è normale.



Next: Lezione 12 (25 marzo
Up: Matematica Discreta
Previous: Lezione 10 (22 marzo
Domenico Luminati
1999-07-08
![]() è riflessiva. Dato che H è un
sottogruppo,
è riflessiva. Dato che H è un
sottogruppo, ![]() e dato che g=gi si ha che
e dato che g=gi si ha che
![]() per ogni
per ogni ![]() .
.
![]() è simmetrica Sia
è simmetrica Sia
![]() ossia esiste
ossia esiste
![]() tale che g2=g1 h, ma allora, moltiplicando a destra per
h-1 si ottiene che
g2h-1=g1h h-1=g11=g1 e dato che H è un
sottogruppo
tale che g2=g1 h, ma allora, moltiplicando a destra per
h-1 si ottiene che
g2h-1=g1h h-1=g11=g1 e dato che H è un
sottogruppo
![]() e quindi
e quindi
![]() .
.
![]() è transitiva. Siano
è transitiva. Siano
![]() e
e
![]() ovvero g2=g1h1 e
g3=g2h2 con
ovvero g2=g1h1 e
g3=g2h2 con
![]() .
Sostituendo la prima
nella seconda si ottiene che
g3=g1h1h2 e dao che H è un
sottogruppo
.
Sostituendo la prima
nella seconda si ottiene che
g3=g1h1h2 e dao che H è un
sottogruppo
![]() e quindi
e quindi
![]() .
.
![]() segue immediatamente dalla definizione di
classe laterale e dalla definizione di classe
d'equivalenza.
segue immediatamente dalla definizione di
classe laterale e dalla definizione di classe
d'equivalenza.
![]()
![]() si denota semplicemente
con
si denota semplicemente
con
![]() e si chiama il quoziente di G modulo H.
e si chiama il quoziente di G modulo H.
![]()
![]() definita da
definita da
![]() .
L'applicazione è surgettiva per definizione di
classe laterale. Dimostriamo che è anche iniettiva. Se
.
L'applicazione è surgettiva per definizione di
classe laterale. Dimostriamo che è anche iniettiva. Se
![]() allora gh1=gh2 e quindi, moltiplicando a sinistra
per g-1 si ottiene
allora gh1=gh2 e quindi, moltiplicando a sinistra
per g-1 si ottiene
![]() ), dato che
queste sono una partizione, si ha che
o(G)=ko(H) e quindi la tesi.
), dato che
queste sono una partizione, si ha che
o(G)=ko(H) e quindi la tesi.
![]()