


Next: Lezione 8 (17 marzo
Up: Matematica Discreta
Previous: Lezione 6 (8 marzo
Subsections
Definizione 7.1
Sia
X un insieme una relazione su
X è un sottoinsieme di
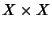
.
Se
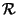
è una relazione su
X si scriverà
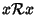
piuttosto che
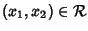
Diremo che
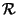
è una
relazione d'equivalenza se verifica
le seguenti proprietà:
- 1.
- (proprietà riflessiva)
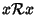 per ogni
per ogni
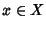 ;
;
- 2.
- (proprietà simmetrica)
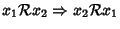 per ogni
per ogni
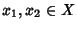 ;
;
- 3.
- (proprietà transitiva)
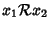 e
e
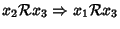 per ogni
per ogni
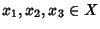 .
.
Se
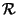
è una relazione d'equivalenza su
X e
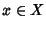
si chiama
classe d'equivalenza di x l'insieme
Osservazione 7.2
Per ogni n la congruenza modulo n è una relazione
d'equivalenza.
Dim.
Si osservi che nella dimostrazione della proposizione 6.5 non si
è usato il fatto che si stesse parlando di congruenze, ma soltanto il
fatto che la relazione di congruenza verifica le proprietà
riflessiva, simmetrica e transitiva; basta allora ripetere parola per
parola quella dimostrazione.

Definizione 7.4
Sia
X un insieme e
una relazione d'equivalenza su
X,
l'insieme delle classi d'equivalenza di
X si chiama
insieme
quoziente di
X modulo
e si denota con
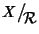
.
È definita l'applicazione
che ad ogni elemento associa la sua classe d'equivalenza e che si chiama
proiezione a quoziente.
Osservazione 7.5
La proiezione a quoziente è evidentemente surgettiva.
Definizione 7.6
Sia
X un'insieme. Un sottoinsieme
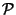
delle parti di
X si dice
una
partizione di
X se:
- 1.
-
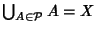 ;
;
- 2.
-
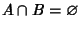 per ogni
per ogni
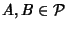 con
con 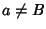 .
.
Esercizio 7.1
Sia
X un insieme. Si dimostri che gli insiemi
sono in bigezione.
Soluzione
Esercizio 7.2
Siano
X e
Y insiemi e sia
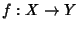
un'applicazione. Si definisca la
relazione su
X
Si provi che
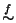
è una relazione d'equivalenza su
X. La
relazione
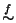
si chiama
relazione indotta da f.
Soluzione
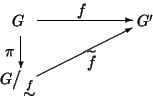
Teorema 7.8
Siano
X,
Y insiemi e
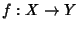
un'applicazione. Esiste una unica
applicazione
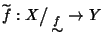
tale che
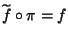
.
Si ha inoltre che:
- 1.
-
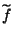 è iniettiva;
è iniettiva;
- 2.
-
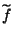 è surgettiva se e solo se f è surgettiva.
è surgettiva se e solo se f è surgettiva.
Dim.
Definiamo
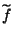 .
Sia
.
Sia
![$\left[x\right]\in X\big/\mathchoice
{{}_{\!\displaystyle {}\stackrel f \sim}}
...
...criptstyle {}\stackrel f \sim}}
{{}_{\!\scriptscriptstyle {}\stackrel f \sim}}$](img266.gif) allora affinché
allora affinché
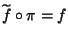 ,
dovrà risultare che
,
dovrà risultare che
![$\widetilde{f{}}(\left[x\right])=\widetilde{f{}}(\pi(x))=f(x)$](img267.gif) .
Quindi se
.
Quindi se
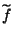 esiste è necessariamente unica e definita da
esiste è necessariamente unica e definita da
![$\widetilde{f{}}(\left[x\right])=f(x)$](img268.gif) .
.
Dimostriamo che questa è una buona definizione, ossia che la definizione non
dipende dal rappresentante della classe, ossia che se
![$\left[x_1\right]=\left[x_2\right]$](img269.gif) allora
allora
![$\widetilde{f{}}(\left[x_1\right])=\widetilde
f(\left[x_2\right])$](img270.gif) .
Ma:
.
Ma:
![\begin{displaymath}\left[x_1\right]=\left[x_2\right]\iff
x_1\stackrel{f}{\sim}x_2\iff
f(x_1)=f(x_2)
\end{displaymath}](img271.gif) |
(1) |
e quindi la definizione è ben posta.
La catena di equivalenze in (1) mostra anche che
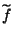 è iniettiva.
è iniettiva.
Supponiamo ora che f sia surgettiva, allora dato 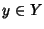 esiste
esiste 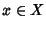 tale che f(x)=y ma allora
tale che f(x)=y ma allora
![$\widetilde{f{}}(\left[x\right])=f(x)=y$](img273.gif) .
Viceversa se
.
Viceversa se
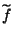 è surgettiva, allora dato
è surgettiva, allora dato 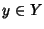 esiste
esiste
![$\left[x\right]\in X\big/\mathchoice
{{}_{\!\displaystyle {}\stackrel f \sim}}
...
...criptstyle {}\stackrel f \sim}}
{{}_{\!\scriptscriptstyle {}\stackrel f \sim}}$](img266.gif) tale che
tale che
![$\widetilde{f{}}(\left[x\right])=y$](img274.gif) .
Ma allora
.
Ma allora
![$f(x)=\widetilde{f{}}(\left[x\right])=y$](img275.gif) ,
ossia f è surgettiva.
,
ossia f è surgettiva.




Next: Lezione 8 (17 marzo
Up: Matematica Discreta
Previous: Lezione 6 (8 marzo
Domenico Luminati
1999-07-08
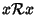 per ogni
per ogni
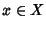 ;
;
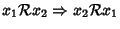 per ogni
per ogni
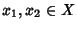 ;
;
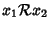 e
e
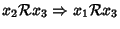 per ogni
per ogni
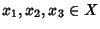 .
.
![]()
![\begin{eqnarray*}\pi_{\cal R}&:& X\longrightarrow{}X\big/\mathchoice
{{}_{\!\di...
...l R}}} \\
\pi_{\cal R}&:& x\longmapsto\left[x\right]_{\cal R}
\end{eqnarray*}](img251.gif)
![]() .
Sia
.
Sia
![]() allora affinché
allora affinché
![]() ,
dovrà risultare che
,
dovrà risultare che
![]() .
Quindi se
.
Quindi se
![]() esiste è necessariamente unica e definita da
esiste è necessariamente unica e definita da
![]() .
.
![]() allora
allora
![]() .
Ma:
.
Ma:
![]() è iniettiva.
è iniettiva.
![]() esiste
esiste ![]() tale che f(x)=y ma allora
tale che f(x)=y ma allora
![]() .
Viceversa se
.
Viceversa se
![]() è surgettiva, allora dato
è surgettiva, allora dato ![]() esiste
esiste
![]() tale che
tale che
![]() .
Ma allora
.
Ma allora
![]() ,
ossia f è surgettiva.
,
ossia f è surgettiva.
![]()