


Next: Lezione 27 (20 maggio
Up: Matematica Discreta
Previous: Lezione 25 (12 maggio
Subsections
Proposizione 26.1
Sia
L un'algebra di Boole. Allora
- 1.
-
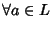 si ha (a')'=a;
si ha (a')'=a;
- 2.
-
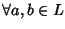 si ha
si ha
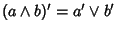 ;
;
- 3.
-
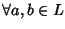 si ha
si ha
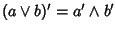 .
.
Le proprietà (2) e (3) vengono chiamate le
leggi di de Morgan.
Dim.
(1). a' è il complemento di a, quindi
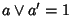 e
e
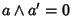 .
Ma
allora, a è un complemento di a', dall'unicità del
complemento segue
allora la tesi.
.
Ma
allora, a è un complemento di a', dall'unicità del
complemento segue
allora la tesi.
(2). Usando le proprietà distributive, commutative di 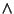 e
e 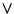 e le
proprietà dello 0 e dell'1 si ha:
e le
proprietà dello 0 e dell'1 si ha:
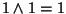 |
= |
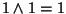 |
(commutativa) |
|
|
= |
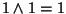 |
(distributiva) |
|
|
= |
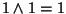 |
(commutativa) |
|
|
= |
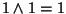 |
(associativa) |
|
|
= |
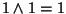 |
(complemento) |
|
|
= |
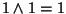 |
(1) |
ed analogamente
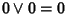 |
= |
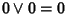 |
(distributiva) |
|
|
= |
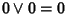 |
(commutativa) |
|
|
= |
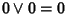 |
(associativa) |
|
|
= |
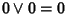 |
(complemento) |
|
|
= |
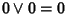 |
(0) |
Quindi
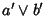 è un complemento di
è un complemento di 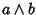 .
Per l'unicità del
complemento si ha la
tesi.
.
Per l'unicità del
complemento si ha la
tesi.
(3). Applichiamo la (2) a a' e b' si ottiene
e quindi per la (1),
Complementando entrambi i membri ed usando di nuovo la (1) si ha allora
che è la tesi.

Sia L un'algebra di Boole, definiamo due operazioni binarie su L ponendo:
Teorema 26.2
Sia
L un'algebra di Boole, allora
L con le operazionei + e
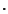
appena definite è un anello booleano.
Dim.
+ è commutativa. Segue immediatamente dalla commutatività di 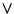 e
e
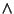 ,
infatti
,
infatti
+ è associativa. Siano
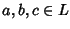 allora, dalla definizione di + si ha
allora, dalla definizione di + si ha
|
(a+b)+c |
= |
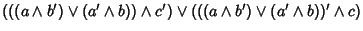 |
|
|
|
|
= |
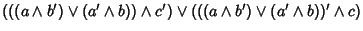 |
|
|
Usando la distributività e l'associatività delle operazioni
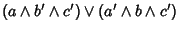 |
= |
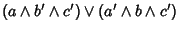 |
|
|
Usando le formule di de Moivre e le altre proprietà
e quindi, in definitiva,
Ma ora, usando la commutatività di + e la formula appena provata, si
ha:
Esistenza dello 0. Lo 0 dell'algebra di boole è anche 0 per
l'anello. Infatti:
Esistenza dell'opposto.
 è associativa. Segue immediatamente dall'associatività di
è associativa. Segue immediatamente dall'associatività di 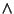 .
.
Proprietà distributiva.
d'altra parte
e quindi
a(b+c)=ab+ac.
Esistenza dell'identità. L'1 dell'algebra è 1 anche per l'anello, dato
che
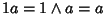 per ogni
per ogni 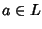 .
.
Ogni elemento è idempotente. Infatti
per ogni 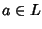 .
.

Il teorema appena dimostrato dà un modo di definire una
struttura di anello booleano a partire da quella di algebra di Boole, mentre
il teorema 25.10 permetteva di fare il percorso inverso, ossia di
ottenere una struttura di algebra di Boole a partire da quella di anello
booleano. Effettivamente queste due costruzioni sono una l'inversa dell'altra,
ossia
Teorema 26.3
Dato un anello booleano costruiamo l'algebra di boole come nel
teorema
25.10 e da questa costruiamo l'anello booleano come nel
teorema precedente, ritroviamo esattamente l'anello da cui si è partiti e
vicersa, data un'algebra di Boole fattone l'anello booleano e quindi
l'algebra di boole, si riottiene l'algebra di Boole di partenza.
Dim.
Sia R un anello booleano, allora la struttura di algebra di Boole è definita da
A partire da questi si definiscono i due nuovi operatori di somma e prodotto
ponendo:
Evidentemente
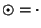 .
Ma, ricordando che un anello booleano
è commutativo e ha caratteristica 2 si ha anche
.
Ma, ricordando che un anello booleano
è commutativo e ha caratteristica 2 si ha anche
e quindi anche
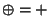 .
.
Viceversa, sia L un'algebra di Boole. La struttura di anello è definita
da:
a partire dalla quale viene definita una struttura di algebra di boole ponendo
Chiaramente
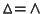 .
D'altra parte
.
D'altra parte
e quindi anche
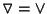 .
.

Osservazione 26.4
Se
X è un insieme allora le due strutture su
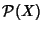
di
algebra di Boole e di
anello booleano definite
rispettivamente dalle operazioni
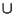
,
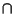
,
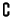
e
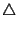
,
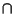
sono in corrispondenza come dal
teorema precedente.
Questo segue evidentemente dalle formule:
la prima delle quali è la definizione di
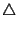
mentre la seconda e la
terza sono di
immediata verifica.
Definizione 26.5
Siano
B e
B' algebre di Boole, diremo che un'applicazione
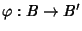
è un
morfismo di algebre di boole se per ogni
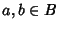
si ha
Si dirà che
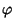
è un
isomorfismo se e solo se è bigettivo.
Esercizio 26.1
Si provi che se
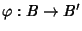
è un morfismo di algebre di Boole allora
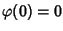
e
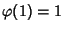
.
Soluzione
Si dimostra la seguente
Proposizione 26.6
Siano
B e
B' due algebre di Boole, allora
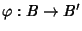
è un morfismo
di algebre di boole se e solo se è un morfismo di anelli per le rispettive
strutture di anello booleano.
Osservazione 26.7
La proposizione precedente mostra che il teorema
26.3 non solo dà
una corrispondenza tra struttura di algebra di Boole e struttura di anello
booleano, ma che tale corrispondenza non cambia l'insieme dei morfismi,
in altre parole le due teorie da una parte quella degli anelli booleani e
dall'altra quella delle algebre di Boole sono due facce della stessa
medaglia e si possono usare contemporaneamente e tutti i risultati di una si
traducono in risultati dell'altra.
Definizione 26.8
Sia
L un reticolo diremo che un sottoinsieme non vuoto
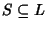
è
un
sottoreticolo se e solo se
- 1.
-
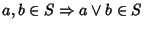
- 2.
-
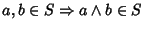
Se
L è un'algebra di Boole, diremo che
S è una
sottoalgebra di
Boole se in più
- 1.
-
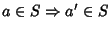
Esercizio 26.2
Si provi che se
L è un reticolo e
S è un sottoreticolo di
L allora
S munito dell'ordinamento indotto da quello di
L è un reticolo.
Soluzione
Osservazione 26.9
Visto l'esercizio precedente e tenendo conto che i reticoli possono essere
definiti anche a partire dall'ordine, verrebbe voglia di prendere quella
data nell'esercizio come definizione. In realtà in generale non è detto
che
S sia un sottoreticolo pur essendo un reticolo con l'ordinamento
indotto. Affinché
S sia un sottoreticole, è necessario anche che
l'estremo inferiore (risp. superiore) fatto in
S coincida con quello fatto
in
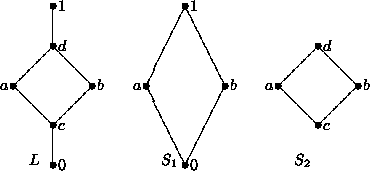
L.Si consideri ad esempio il reticolo
L rappresentato nel diagramma
di figura
1. Allora
S1, pur essendo un reticolo con
l'ordinamento indotto, non è un sottoreticolo: l'estremo inferiore tra
a e
b fatto in
S1 è ), mentre fatto in
L è
c.
S2 è invece
un sottoreticolo.
Figure 1:
S2 è un sottoreticolo di L ma non S1
 |
Proposizione 26.10
Sia
B un'algebra di Boole, allora
S è una sottoalgebra se e solo se
è un sottoanello per la struttura di anello booleano.
Osservazione 26.11
La proposizione precedente mostra come anche la nozione di sottostruttura
sia conservata dalla corrispondenza data dal teorema
26.3.
Esercizio 26.3
Si provi che se
S è una sottoalgebra dell'algebra di Boole
B, allora
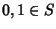
.
Soluzione
Teorema 26.12
Sia
L un'algebra di Boole. Allora esiste un insieme
X tale che
L è
isomorfa ad una sottoalgebra di
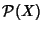
.
Se
L è finita allora esiste
X tale che
L è isomorfa a
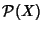
.
Dim.
È conseguenza immediata del teorema di rappresentazione per
anelli booleani di quanto visto nelle proposizioni 26.6 e
26.10 e di quanto osservato in 26.4. Infatti per ilteorema di
rappresentazione degli anelli booleani esiste un morfismo iniettivo di anelli
booleani
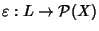 per un opportuno insieme X, che è anche
surgettivo quando L è finito. Allora
per un opportuno insieme X, che è anche
surgettivo quando L è finito. Allora
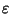 è un morfismo di algebre di
Boole quando si considerino le strutture corrispondenti, e quindi la tesi.
è un morfismo di algebre di
Boole quando si considerino le strutture corrispondenti, e quindi la tesi.

Esempio 26.14
Si consideri il reticolo
L rappresentato nel diagramma di figurafig:S<L.
Ci chiediamo: è un 'algebra di Boole? Per il
corollario
precedente, la risposta è chiaramente no, in quanto questo
reticolo ha 6 elementi e 6 non è una potenza di 2.



Next: Lezione 27 (20 maggio
Up: Matematica Discreta
Previous: Lezione 25 (12 maggio
Domenico Luminati
1999-07-08
![]() e
e
![]() .
Ma
allora, a è un complemento di a', dall'unicità del
complemento segue
allora la tesi.
.
Ma
allora, a è un complemento di a', dall'unicità del
complemento segue
allora la tesi.
![]() e
e ![]() e le
proprietà dello 0 e dell'1 si ha:
e le
proprietà dello 0 e dell'1 si ha:
![]() e
e
![]() ,
infatti
,
infatti
![]() allora, dalla definizione di + si ha
allora, dalla definizione di + si ha
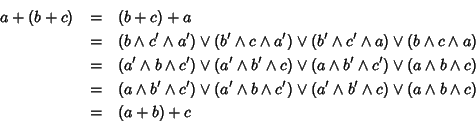
![]() è associativa. Segue immediatamente dall'associatività di
è associativa. Segue immediatamente dall'associatività di ![]() .
.
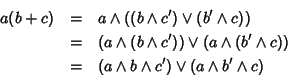
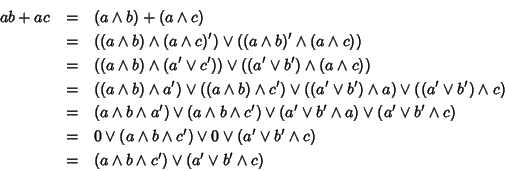
![]() per ogni
per ogni ![]() .
.
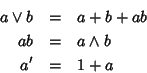
![]() .
Ma, ricordando che un anello booleano
è commutativo e ha caratteristica 2 si ha anche
.
Ma, ricordando che un anello booleano
è commutativo e ha caratteristica 2 si ha anche
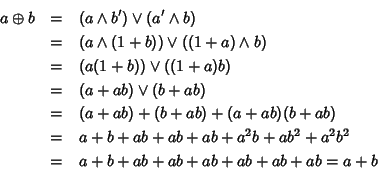
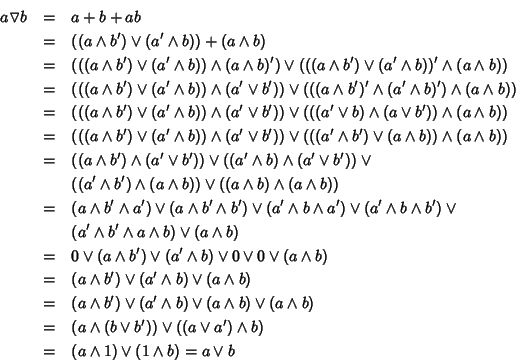
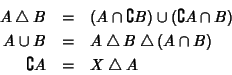
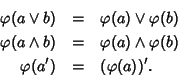
![]() per un opportuno insieme X, che è anche
surgettivo quando L è finito. Allora
per un opportuno insieme X, che è anche
surgettivo quando L è finito. Allora
![]() è un morfismo di algebre di
Boole quando si considerino le strutture corrispondenti, e quindi la tesi.
è un morfismo di algebre di
Boole quando si considerino le strutture corrispondenti, e quindi la tesi.
![]()