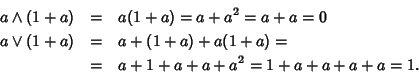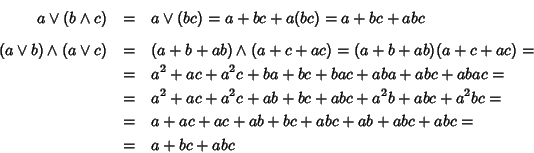Next: Lezione 26 (17 maggio
Up: Matematica Discreta
Previous: Lezione 24 (10 maggio
Subsections
Abbiamo visto in precedenza che se 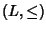 è un reticolo, allora sono
definite le due operazioni binarie
è un reticolo, allora sono
definite le due operazioni binarie
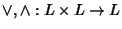 che verificano
le proprietà commutativa, associativa e di
assorbimento. Vediamo come tali proprietà delle due operazioni determinino
la struttura del reticolo.
che verificano
le proprietà commutativa, associativa e di
assorbimento. Vediamo come tali proprietà delle due operazioni determinino
la struttura del reticolo.
Teorema 25.1
Sia
L un insieme su cui sono definite due operazioni binarie
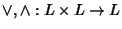
tali che per ogni
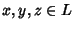
si abbia:
Allora esiste un ordinamento
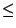
su
L che rende
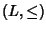
un reticolo
tale che per ogni
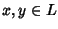
si ha che
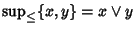
e
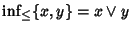
.
Dim.
L'esercizio 24.1 ci dice come definire la relazione
d'ordine. Definiamo:
Proviamo che 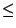 è una relazione d'equivalenza.
è una relazione d'equivalenza.
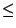 è riflessiva. Usando la proprietà di assorbimento
si ha che
è riflessiva. Usando la proprietà di assorbimento
si ha che
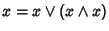 e quindi
e quindi
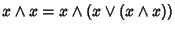 .
Ma allora usando ancora la proprietà di assorbimento
.
Ma allora usando ancora la proprietà di assorbimento
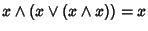 e quindi
e quindi
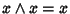 ossia
ossia 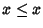 .
.
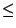 è antisimmetrica. Siano
è antisimmetrica. Siano 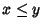 e
e 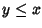 ,
ossia
,
ossia
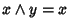 e
e
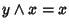 .
Per la commutatività si ha allora che
.
Per la commutatività si ha allora che
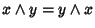 e quindi x=y.
e quindi x=y.
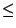 è transitiva. Sia
è transitiva. Sia 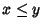 e
e 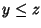 ossia
ossia
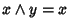 e
e
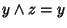 .
Allora, usando l'associatività,
.
Allora, usando l'associatività,
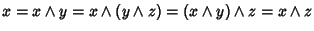 e quindi
e quindi 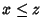 .
.
Proviamo ora che 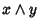 è l'estremo inferiore tra x e y. Usando la
commutatività, l'associatività ed il già provato fatto che per ogni
è l'estremo inferiore tra x e y. Usando la
commutatività, l'associatività ed il già provato fatto che per ogni
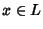 si ha
si ha
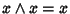 ,
si ha
,
si ha
Sia ora 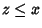 e
e 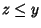 ,
ossia
,
ossia
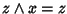 e
e
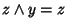 ,
allora
,
allora
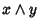 verifica quindi le proprietà
caratterizzanti
dell'estremo inferiore, e quindi è l'estremo inferiore.
verifica quindi le proprietà
caratterizzanti
dell'estremo inferiore, e quindi è l'estremo inferiore.
Proviamo ora che 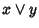 è l'estremo superiore tra x e y. Usando le
proprietà commutative e di assorbimento, si ha
è l'estremo superiore tra x e y. Usando le
proprietà commutative e di assorbimento, si ha
Sia ora 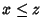 e
e 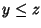 ossia
ossia
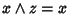 e
e
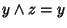 .
Allora, usando
le proprietà di assorbimento e la commutatività, si ha che da
.
Allora, usando
le proprietà di assorbimento e la commutatività, si ha che da
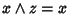 si ha che
si ha che
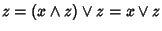 e, analogamente,
e, analogamente,
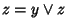 ,
ma allora, usando queste relazioni, l'associatività e la
proprietà di assorbimento, si ha
,
ma allora, usando queste relazioni, l'associatività e la
proprietà di assorbimento, si ha
Questo, prova che 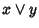 è l'estremo superiore tra x e
y.
è l'estremo superiore tra x e
y.
Si poteva anche osservare che dalle tre proprietà si ricava che
 (si veda l'esercizio seguente), ossia
(si veda l'esercizio seguente), ossia 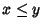 se e solo se
se e solo se 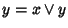 .
L'ultima proprietà poteva più semplicemente
essere mostrata nel seguente modo: se
.
L'ultima proprietà poteva più semplicemente
essere mostrata nel seguente modo: se 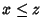 e
e 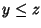 allora
allora 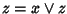 e
e
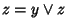 ,
ma allora
,
ma allora

Osservazione 25.2
La proposizione
24.7 ed il
teorema precedente
mostrano che è completamente equivalente definire un reticolo in
termini di ordinamento oppure definirlo come insieme dotato di due operazioni
commutative, associative e che verificano la proprietà di assorbimento. Le
due strutture algebrica (data dalle proprietà delle operazioni) e d'ordine
sono due facce della stessa medaglia e che possono quindi essere usate
indifferentemente a seconda delle necessità.
Esercizio 25.1
Si dimostri usando soltanto le proprietà commutativa, associativa e di
assorbimento delle due operazioni, che in un reticolo

.
Soluzione
Definizione 25.3
Sia
L un reticolo diremo che
L è
limitato se ha massimo e
minimo, che saranno denotati rispettivamente con 0 e 1. Ossia, nel
linguaggio dell'ordinamento
o, equivalentemente, nel linguaggio algebrico
che, in virtù di quanto visto nell'esercizio
24.1, equivale a dire
Se
L è un reticolo limitato, diremo che
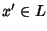
è un
complemento di
x se:
Un reticolo limitato in cui ogni elemento ha un complemento di dice complementato
Osservazione 25.4
Rispetto alla struttura algebrica, lo 0 è elemento neutro per
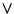
mentre 1 è un elemento neutro per
.
Definizione 25.5
Diremo che un reticolo
L è
distributivo se valgono le seguenti:
Esercizio 25.2
Sia
L un reticolo. Si provi che le due proposizioni
- 1.
-
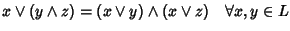
- 2.
-
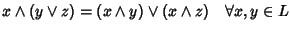
sono equivalenti.
In altri termini, nella definizione che abbiamo dato una delle due richieste
è superflua, e quindi per verificare che un reticolo è distributivo è
sufficiente mostrarne una delle due.
Soluzione
Proposizione 25.6
Sia
L un reticolo distributivo e limitato. Se
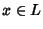
ha un complemento,
allora tale complemento è unico.
Dim.
Supponiamo che x1 e x2 siano due complementi di x, allora
scambiando x1 con x2 si ottiene anche
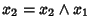 e quindi,
x1=x2.
e quindi,
x1=x2.

Osservazione 25.7
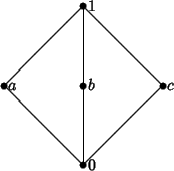
La distributività è essenziale per l'unicità del complemento. Si
prenda ad esempio il reticolo schemattizzato dal seguente diagramma:
intendendo con questo che
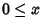
e
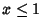
per ogni
x e che
a,
b,
c non sono tra loro confrontabili. Allora chiaramente sia
b che
c sono dei
complementi per
a ed infatti il reticolo non è distributivo:
mentre
Definizione 25.8
Un reticolo distributivo, e complementato viene chiamato un'
algebra di
Boole.
Esempio 25.9
Se
X è un insieme il reticolo
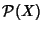
delle sue parti è un'algebra di
Boole. Valgono infatti le relazioni di distributività ed il complemento di
un
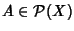
non è altro che il suo complementare insiemistico
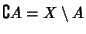
.
Dim.
Dobbiamo dimostrare che R è limitato, complementato e
distributivo. Ricordiamo che la struttura di reticolo di Rè data dll'ordinamento parziale
 per la quale si ha
per la quale si ha
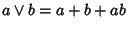 e
e
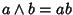 .
.
Osserviamo che
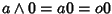 per ogni
per ogni 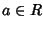 e quindi lo 0 dell'anello
è anche lo 0 del reticolo.
e quindi lo 0 dell'anello
è anche lo 0 del reticolo.
Se 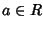 allora
allora
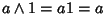 e quindi l'1 dell'anello è anche
l'1 del reticolo.
e quindi l'1 dell'anello è anche
l'1 del reticolo.
Se 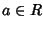 allora
allora
quindi (1+a) è un complemento di a.
Proviamo che è distributivo.
e quindi
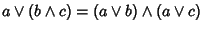 .
Per quanto detto
nell'esercizio 25.2, possiamo allora affermare che il reticolo è
distributivo.
.
Per quanto detto
nell'esercizio 25.2, possiamo allora affermare che il reticolo è
distributivo.




Next: Lezione 26 (17 maggio
Up: Matematica Discreta
Previous: Lezione 24 (10 maggio
Domenico Luminati
1999-07-08
![]() è una relazione d'equivalenza.
è una relazione d'equivalenza.
![]() è riflessiva. Usando la proprietà di assorbimento
si ha che
è riflessiva. Usando la proprietà di assorbimento
si ha che
![]() e quindi
e quindi
![]() .
Ma allora usando ancora la proprietà di assorbimento
.
Ma allora usando ancora la proprietà di assorbimento
![]() e quindi
e quindi
![]() ossia
ossia ![]() .
.
![]() è antisimmetrica. Siano
è antisimmetrica. Siano ![]() e
e ![]() ,
ossia
,
ossia
![]() e
e
![]() .
Per la commutatività si ha allora che
.
Per la commutatività si ha allora che
![]() e quindi x=y.
e quindi x=y.
![]() è transitiva. Sia
è transitiva. Sia ![]() e
e ![]() ossia
ossia
![]() e
e
![]() .
Allora, usando l'associatività,
.
Allora, usando l'associatività,
![]() e quindi
e quindi ![]() .
.
![]() è l'estremo inferiore tra x e y. Usando la
commutatività, l'associatività ed il già provato fatto che per ogni
è l'estremo inferiore tra x e y. Usando la
commutatività, l'associatività ed il già provato fatto che per ogni
![]() si ha
si ha
![]() ,
si ha
,
si ha
![]() e
e ![]() ,
ossia
,
ossia
![]() e
e
![]() ,
allora
,
allora
![]() è l'estremo superiore tra x e y. Usando le
proprietà commutative e di assorbimento, si ha
è l'estremo superiore tra x e y. Usando le
proprietà commutative e di assorbimento, si ha
![]() e
e ![]() ossia
ossia
![]() e
e
![]() .
Allora, usando
le proprietà di assorbimento e la commutatività, si ha che da
.
Allora, usando
le proprietà di assorbimento e la commutatività, si ha che da
![]() si ha che
si ha che
![]() e, analogamente,
e, analogamente,
![]() ,
ma allora, usando queste relazioni, l'associatività e la
proprietà di assorbimento, si ha
,
ma allora, usando queste relazioni, l'associatività e la
proprietà di assorbimento, si ha
![]() (si veda l'esercizio seguente), ossia
(si veda l'esercizio seguente), ossia ![]() se e solo se
se e solo se ![]() .
L'ultima proprietà poteva più semplicemente
essere mostrata nel seguente modo: se
.
L'ultima proprietà poteva più semplicemente
essere mostrata nel seguente modo: se ![]() e
e ![]() allora
allora ![]() e
e
![]() ,
ma allora
,
ma allora
![]() per la quale si ha
per la quale si ha
![]() e
e
![]() .
.
![]() per ogni
per ogni ![]() e quindi lo 0 dell'anello
è anche lo 0 del reticolo.
e quindi lo 0 dell'anello
è anche lo 0 del reticolo.
![]() allora
allora
![]() e quindi l'1 dell'anello è anche
l'1 del reticolo.
e quindi l'1 dell'anello è anche
l'1 del reticolo.
![]() allora
allora