Next: Soluzione degli esercizi proposti
Up: Matematica Discreta
Previous: Lezione 26 (17 maggio
Subsections
Definizione 27.1
Sia
A un insieme e
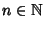
,
una
operazione n-aria su
A non è
altro che un'applicazione
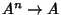
.
Quindi l'insieme delle applicazioni
n-arie su
A altri non è che
AAn.
Osservazione 27.2
Operazioni binarie (i.e. 2-arie) se ne sono incontrate a non finire (le
operazioni di un gruppo, di un anello, di un reticolo), anche
di operazioni 1-arie, ossia di funzioni, ad esempio il complemento in
un'algebra di Boole, l'inverso in un gruppo sono operazioni 1-arie.
Cerchiamo di capire cosa sono le operazioni 0-arie. Si pone, per
definizione,
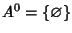
,
ossia l'insieme che ha come unico elemento
l'insieme vuoto, allora una operazione 0-aria su
A non è altro che
un'applicazione
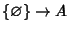
ossia è fissare un elemento di
A. Ma
allora anche di operazioni 0-arie se ne sono già incontrate tante:
l'unità di un monoide è un'operazione 0-aria (si fissa un particolare
elemento del monoide), lo 0 e l'1 di un anello con identità o di
un'algebra di Boole sono operazioni 0-arie.
Definizione 27.3
Sia
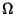
un insieme e sia
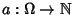
un'applicazione. Chiameremo
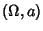
un
dominio di operatori e dato
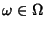
diremo
che
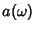
è la
arietà di
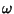
.
Indichereamo con
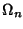
l'insieme degli
omega che hanno arietà pari a
n, ossia
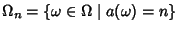
.
Definizione 27.4
Sia
A un insieme una struttura di
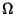
-algebra su
A è il dato per
ogni
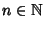
di un'applicazione
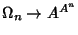
.
In pratica si interpreta ogni elemento di 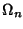 come una operazione
n-aria su A. Se
come una operazione
n-aria su A. Se
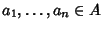 e
e
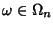 si indica con
si indica con
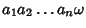 il risultato dell'operazione rappresentata da
il risultato dell'operazione rappresentata da
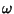 sulla n-pla
sulla n-pla
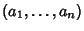 .
Questo tipo di notazione è
conosciuta come notazione polacca inversa ed è comoda in quanto non
necessita dell'utilizzo delle parentesi: ogni volta che si trova scritto un
operatore n-ario, lo si fa agire sugli n elementi di A che lo precedono.
.
Questo tipo di notazione è
conosciuta come notazione polacca inversa ed è comoda in quanto non
necessita dell'utilizzo delle parentesi: ogni volta che si trova scritto un
operatore n-ario, lo si fa agire sugli n elementi di A che lo precedono.
Esempio 27.5
I semigruppi. Sia
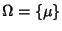
costituito da un solo elemento,
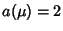
.
Allora un semigruppo è una
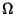
-algebra tale che
Si osservi che questa è la traduzione in notazione polacca inversa della
relazione che definisce la
associativa proprietà.
I monoidi. Sia
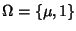
con
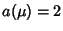
e
a(1)=0. Un monoide è
una
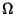
-algebra in cui oltre alla proprietà associativa si ha
L'operatore 0-ario 1 è l'identità del monoide e la formula appena
scritta è la traduzione delle
proprietà
dell'identità.
I gruppi. Sia
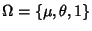 con
con 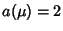 ,
,
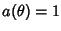 e
a(1)=0. Un gruppo è una
e
a(1)=0. Un gruppo è una 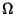 -algebra in cui valgono le due
precedenti e
-algebra in cui valgono le due
precedenti e
Questa è la traduzione delle proprietà dell'inverso, ossia
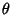
è
interpretato come l'operazione 1-aria che ad ogni elemento associa il suo
inverso.
In modo analogo si vede che tutte le strutture algebr2iche che abbiamo preso
in considerazione (anelli, reticoli, algebre di boole) rientrano in questo
quadro generale.
Definizione 27.6
Siano
A e
B due
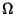
-algebre un'applicazione
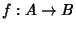
è detta
un
morfismo se:
Dove si è usata la notazione polacca anche per
f, ossia
af significa
l'immagine di
a tramite
f ossia quello che abbiamo sempre denotato con
f(
a).
Ossia applicare f a ogni elemento e quindi applicare l'operazione su Brappresentata da 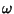 è lo stesso che prima applicare l'operazione su
A rappresentata da
è lo stesso che prima applicare l'operazione su
A rappresentata da 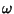 ad ogni elemento e quindi applicare f al
risultato. Chiaramente la definizione di morfismo che abbiamo appena dato
congloba tutte le definizioni di morfismo che abbiamo dato per ogni struttura.
ad ogni elemento e quindi applicare f al
risultato. Chiaramente la definizione di morfismo che abbiamo appena dato
congloba tutte le definizioni di morfismo che abbiamo dato per ogni struttura.
Definizione 27.7
Sia
A una
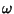
-algebra. Diremo che
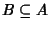
è una
sotto
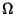 -algebra
-algebra se
Detto in altri termini B è chiuso rispetto a tutte le operazioni di A.
Anche questa definizione chiaramente ingloba tutte le definizioni di
sottostruttura che abbiamo dato.
Definizione 27.8
Sia
A una
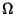
-algebra, diremo che una relazione d'equivalenza
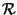
su
A è una
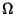 -congruenza
-congruenza (brevemente una congruenza) se per
ogni
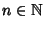
,
per ogni
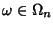
e per ogni
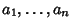
,
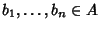
Si osservi che questa che abbiamo dato come definizione è esattamente la
proprietà che ci è servita nel caso dei gruppi e degli anelli per definire una struttura di gruppo e di anello sul
quoziente in modo che la proiezione a quoziente sia un morfismo. Usando
esattamente la stessa dimostrazione fatta in questi due casi, si prova allora
il seguente teorema:
Teorema 27.9
Sia
A una
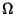
-algebra e sia
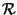
una
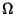
-congruenza su
A,
allora esiste una unica struttura di
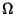
-algebra su
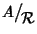
che rende la proiezione a quoziente un morfismo.
Tale struttura è definita ponendo per ogni
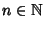 ,
,
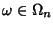 e
e
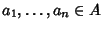 :
:
Esercizio 27.1
Descrivere in termini di
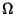
-algebre le strutture di anello, reticolo,
algebra di Boole.
Soluzione
Esercizio 27.2
Siano
A e
B due
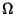
algebre e sia
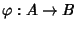
un morfismo. Si
consideri la relazione d'equivalenza
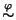
indotta su
A da
f. Si provi che
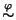
è una congruenza.
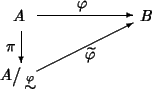
Si provi inoltre che esiste un unico morfismo di
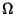
-algebre
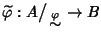
tale che
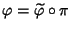
.
Si ha inoltre che:
- 1.
-
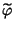 è iniettiva;
è iniettiva;
- 2.
-
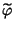 è surgettiva se e solo se
è surgettiva se e solo se 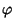 è surgettiva.
è surgettiva.
Soluzione



Next: Soluzione degli esercizi proposti
Up: Matematica Discreta
Previous: Lezione 26 (17 maggio
Domenico Luminati
1999-07-08
![]() come una operazione
n-aria su A. Se
come una operazione
n-aria su A. Se
![]() e
e
![]() si indica con
si indica con
![]() il risultato dell'operazione rappresentata da
il risultato dell'operazione rappresentata da
![]() sulla n-pla
sulla n-pla
![]() .
Questo tipo di notazione è
conosciuta come notazione polacca inversa ed è comoda in quanto non
necessita dell'utilizzo delle parentesi: ogni volta che si trova scritto un
operatore n-ario, lo si fa agire sugli n elementi di A che lo precedono.
.
Questo tipo di notazione è
conosciuta come notazione polacca inversa ed è comoda in quanto non
necessita dell'utilizzo delle parentesi: ogni volta che si trova scritto un
operatore n-ario, lo si fa agire sugli n elementi di A che lo precedono.
![]() con
con ![]() ,
,
![]() e
a(1)=0. Un gruppo è una
e
a(1)=0. Un gruppo è una ![]() -algebra in cui valgono le due
precedenti e
-algebra in cui valgono le due
precedenti e
![]() ,
,
![]() e
e
![]() :
: