


Next: Lezione 23 (5 maggio
Up: Matematica Discreta
Previous: Lezione 21 (29 aprile
Subsections
Definizione 22.1
Sia
R un anello con identità, si dice che
R è un
anello booleano,
o anche
anello di Boole, se
Esempio 22.2
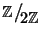
è un anello booleano, infatti 0
2=0 e 1
2=1 e
0 e 1 sono gli unici elementi di
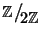
.
Esempio 22.3
Sia
X un insieme, l'anello
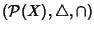
è un anello booleano.
Infatti
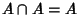
per ogni
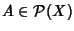
.
Esercizio 22.1
Si provi che se
R è un anello booleano e
X è un insieme, allora
RX è un anello booleano.
Soluzione
Esercizio 22.2
Sia
X un insieme, si provi che l'anello
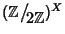
è
isomorfo a
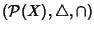
.
Soluzione
Dim.
(1). Sia 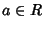 allora
a=a2=(-a)2=-a, quindi a+a=0. In particolare
1+1=0, ossia
allora
a=a2=(-a)2=-a, quindi a+a=0. In particolare
1+1=0, ossia
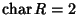 .
.
(2). Siano 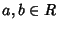 allora,
allora,
a+b=(a+b)2=a2+ab+ba+b2 = a + ab + ba + b
da cui si ricava che
ab + ba = 0 e quindi ab = -ba. Per quanto visto al
punto precedente -ba=ba e quindi ab = ba.

Esercizio 22.3
Sia
R un anello booleano. Si provi che l'unico elemento invertibile di
R è 1.
Soluzione
Esercizio 22.4
Sia
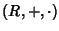
un anello booleano, si provi che anche
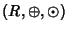
è un anello booleano, essendo
Soluzione
Definizione 22.5
Sia
R un anello commutativo con identità, diremo che un ideale
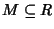
è
massimale se
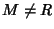
e gli unici ideali
I tali
che
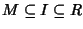
sono
I e
R. In simboli
Proposizione 22.6
Sia
R un anello commutativo con identità e
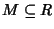
un ideale.
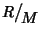
è un campo se e solo se
M è massimale.
Dim.
Supponiamo che M sia massimale e sia
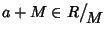 diverso da
0+M ossia
diverso da
0+M ossia 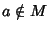 .
Consideriamo l'insieme
.
Consideriamo l'insieme
I è un ideale (si vedano gli esercizi 15.3, 15.4 e 15.5),
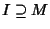 e
e 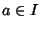 quindi
quindi 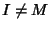 ,
per la massimalità di M allora I=R e quindi
,
per la massimalità di M allora I=R e quindi 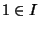 ,
ossia esiste
,
ossia esiste 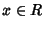 e
e 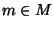 tale che 1= ax + m ossia ax+M=1+M e
pertanto
(a+M)(x+M)=1+M, ovvero a+M è invertibile.
tale che 1= ax + m ossia ax+M=1+M e
pertanto
(a+M)(x+M)=1+M, ovvero a+M è invertibile.
Supponiamo ora che
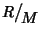 sia un campo. Sia
sia un campo. Sia
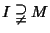 un
ideale, e sia
un
ideale, e sia
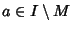 .
Dato che
.
Dato che
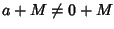 e
e
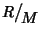 è un campo, allora esiste x+M tale che
(a+M)(x+M)=1+M ossia tale che
è un campo, allora esiste x+M tale che
(a+M)(x+M)=1+M ossia tale che
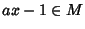 .
Ma allorea esiste un
.
Ma allorea esiste un 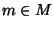 tale che ax-1=m e quindi
1=m-ax. Ora,
tale che ax-1=m e quindi
1=m-ax. Ora,
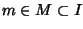 ,
,
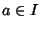 e quindi
e quindi 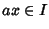 ,
per cui
,
per cui 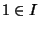 .
Da ciò segue che I=R e quindi M è massimale.
.
Da ciò segue che I=R e quindi M è massimale.

Vale il seguente teorema di cui omettiamo la dimostrazione:
Teorema 22.7
Sia
R un anello e sia
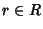
un elemento non invertibile. Allora esiste un
ideale massimale di
R che contiene
r.
Lemma 22.8
Sia
R un anello booleano e sia
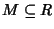
un ideale massimale. Allora
per ogni
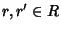
si ha
- 1.
-
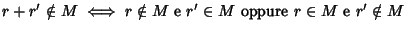
- 2.
-
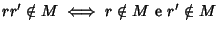
Dim.
Sia
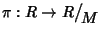 la proiezione a quoziente, allora per ogni
la proiezione a quoziente, allora per ogni
 si ha a2-a=0 e quindi
si ha a2-a=0 e quindi
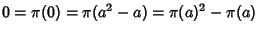 ,
ossia
per ogni
,
ossia
per ogni
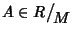 si ha A2-A=0 ossia A(A-1)=0. Ma ora, dato
che M è massimale,
si ha A2-A=0 ossia A(A-1)=0. Ma ora, dato
che M è massimale,
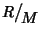 è un campo, in particolare è un dominio di
integrità e
pertanto da A(A-1)=0 si deduce che A=0 oppure A=1.
è un campo, in particolare è un dominio di
integrità e
pertanto da A(A-1)=0 si deduce che A=0 oppure A=1.
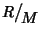 ha solo i due elementi 0+M e 1+M, è quindi isomorfo a
ha solo i due elementi 0+M e 1+M, è quindi isomorfo a
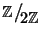 ,
e quindi per ogni
,
e quindi per ogni
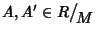 si ha:
si ha:
che possono essere riscritte
Ma allora la tesi si ottiene prendendo A = r + M e A'=r'+M e ricordando
che per ogni 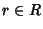 si ha r+M=0+M se e solo se
si ha r+M=0+M se e solo se 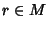 .
.

Indichiamo con
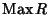 l'insieme degli ideali massimali di R e consideriamo
l'applicazione
l'insieme degli ideali massimali di R e consideriamo
l'applicazione
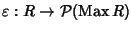 definita da:
definita da:
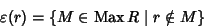 |
(28) |
Teorema 22.9 (di rappresentazione)
Sia
R un anello booleano. Allora l'applicazione
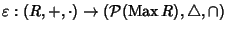 definita
sopra
definita
sopra è un morfismo iniettivo di anelli con identità.
Se
R è finito,
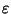
è anche surgettiva, e quindi un isomorfismo.



Next: Lezione 23 (5 maggio
Up: Matematica Discreta
Previous: Lezione 21 (29 aprile
Domenico Luminati
1999-07-08
![]() allora
a=a2=(-a)2=-a, quindi a+a=0. In particolare
1+1=0, ossia
allora
a=a2=(-a)2=-a, quindi a+a=0. In particolare
1+1=0, ossia
![]() .
.
![]() allora,
allora,
![]() diverso da
0+M ossia
diverso da
0+M ossia ![]() .
Consideriamo l'insieme
.
Consideriamo l'insieme
![]() sia un campo. Sia
sia un campo. Sia
![]() un
ideale, e sia
un
ideale, e sia
![]() .
Dato che
.
Dato che
![]() e
e
![]() è un campo, allora esiste x+M tale che
(a+M)(x+M)=1+M ossia tale che
è un campo, allora esiste x+M tale che
(a+M)(x+M)=1+M ossia tale che
![]() .
Ma allorea esiste un
.
Ma allorea esiste un ![]() tale che ax-1=m e quindi
1=m-ax. Ora,
tale che ax-1=m e quindi
1=m-ax. Ora,
![]() ,
,
![]() e quindi
e quindi ![]() ,
per cui
,
per cui ![]() .
Da ciò segue che I=R e quindi M è massimale.
.
Da ciò segue che I=R e quindi M è massimale.
![]()
![]() la proiezione a quoziente, allora per ogni
la proiezione a quoziente, allora per ogni
![]() si ha a2-a=0 e quindi
si ha a2-a=0 e quindi
![]() ,
ossia
per ogni
,
ossia
per ogni
![]() si ha A2-A=0 ossia A(A-1)=0. Ma ora, dato
che M è massimale,
si ha A2-A=0 ossia A(A-1)=0. Ma ora, dato
che M è massimale,
![]() è un campo, in particolare è un dominio di
integrità e
pertanto da A(A-1)=0 si deduce che A=0 oppure A=1.
è un campo, in particolare è un dominio di
integrità e
pertanto da A(A-1)=0 si deduce che A=0 oppure A=1.
![]() ha solo i due elementi 0+M e 1+M, è quindi isomorfo a
ha solo i due elementi 0+M e 1+M, è quindi isomorfo a
![]() ,
e quindi per ogni
,
e quindi per ogni
![]() si ha:
si ha:
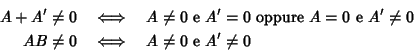
![]() l'insieme degli ideali massimali di R e consideriamo
l'applicazione
l'insieme degli ideali massimali di R e consideriamo
l'applicazione
![]() definita da:
definita da: