Soluzione dell'esercizio 7.1 Per quanto visto nell'osservazione 7.7, possiamo definire l'applicazione
Soluzione dell'esercizio 7.1 Per quanto visto nell'osservazione 7.7, possiamo definire
l'applicazione
![]() data da
data da
![]() .
.
Data invece una partizione
![]() definiamo la relazione
definiamo la relazione
![]() ponendo
ponendo
![]() è riflessiva. Se
è riflessiva. Se ![]() allora, dato che
allora, dato che ![]() ricopre X, esiste
ricopre X, esiste
![]() tale che
tale che ![]() e quindi
e quindi
![]() .
.
![]() è simmetrica. Ovvio.
è simmetrica. Ovvio.
![]() è transitiva. Siano
è transitiva. Siano
![]() e
e
![]() ,
allora esistono
,
allora esistono
![]() tali che
tali che
![]() e
e
![]() .
Ma, allora
.
Ma, allora
![]() ossia
ossia
![]() e quindi coincidono, ossia A=B e quindi
e quindi coincidono, ossia A=B e quindi
![]() ovvero
ovvero
![]() .
.
Definiamo allora
![]() ponendo
ponendo
![]() ,
e
proviamo che
,
e
proviamo che
![]() e
e
![]() .
Ciò concluderà la
dimostrazione.
.
Ciò concluderà la
dimostrazione.
Sia
![]() ,
allora, per la 2 della proposizione 7.3,
si ha che
,
allora, per la 2 della proposizione 7.3,
si ha che
![]() se e solo se
se e solo se
![]() ossia se e solo se esiste
ossia se e solo se esiste
![]() tale che
tale che
![]() ossia se e solo se esiste
ossia se e solo se esiste
![]() tale che
tale che
![]() ossia se e
solo se
ossia se e
solo se
![]() e quindi
e quindi
![]() .
.
Sia invece
![]() ,
allora, dato
,
allora, dato ![]() sia
sia ![]() ,
è chiaro che
,
è chiaro che
![]() ,
ciò unito al fatto che
,
ciò unito al fatto che ![]() ricopre X permette di concludere che
ricopre X permette di concludere che
![]() ovvero che
ovvero che
![]() .
.
![]()
Soluzione dell'esercizio 7.2
![]() è riflessiva. Se
è riflessiva. Se ![]() allora, f(x)=f(x) e quindi
allora, f(x)=f(x) e quindi
![]() .
.
![]() è simmetrica. Ovvio.
è simmetrica. Ovvio.
![]() è transitiva. Siano
è transitiva. Siano
![]() e
e
![]() ,
allora
f(x1)=f(x2) e
f(x2)=f(x3) da cui
segue immediatamente che
f(x1)=f(x3) e quuindi
,
allora
f(x1)=f(x2) e
f(x2)=f(x3) da cui
segue immediatamente che
f(x1)=f(x3) e quuindi
![]() .
.
![]()
Soluzione dell'esercizio 8.1 (1). Siano
![]() e sia
e sia ![]() ,
allora, usando
l'associatività di * si ha:
,
allora, usando
l'associatività di * si ha:
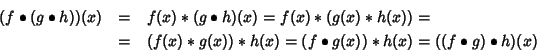
(2). Sia ![]() la funzione 1(x)=1Y per ogni
la funzione 1(x)=1Y per ogni ![]() ,
essendo 1Yl'unità di Y.. Allora per ogni
,
essendo 1Yl'unità di Y.. Allora per ogni ![]() e per ogni
e per ogni ![]() si ha:
si ha:
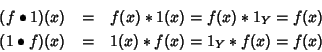
(3). Dato ch eogni elemento di Y ha un inverso, data ![]() possiamo definire la funzione f-1 pomnendo
f-1(x)=(f(x))-1 per ogni
possiamo definire la funzione f-1 pomnendo
f-1(x)=(f(x))-1 per ogni ![]() .
Allora per ogni
.
Allora per ogni ![]() si ha
si ha
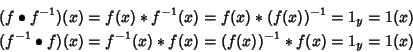
(4). Siano
![]() ,
per la commutatività di * si ha
che per ogni
,
per la commutatività di * si ha
che per ogni ![]()
Soluzione dell'esercizio 8.2 Dal fatto che
gg-1=1=g-1g ne segue che g è un inverso destro e
sinistro di g-1 e quindi per l'unicità
dell'inverso
g=(g-1)-1.
![]()
Soluzione dell'esercizio 8.3 Si ha:
Se il gruppo è commutativo, allora
(g1g2)-1=g2-1g1-1=g1-1g2-1. Viceversa, supponiamo che
(g1g2)-1=g1-1g2-1 per ogni
![]() .
Allora
.
Allora
Soluzione dell'esercizio 8.4 G è chiuso per l'operazione, infatti se
![]() siano
siano
![]() gli inversi, allora
gli inversi, allora
Chiaramente 1 è invertibile e se g è invertibile anche g-1 lo
è.
![]()
Soluzione dell'esercizio 8.5 Verifichiamo che per ogni n si ha che
![]() è un sottogruppo di
è un sottogruppo di
![]() .
.
![]() dato che
dato che
![]() .
Inoltre se
.
Inoltre se
![]() e
e
![]() allora
allora
![]() e quindi si conclude per il
criterio del sottogruppo.
e quindi si conclude per il
criterio del sottogruppo.
Proviamo ora che tutti i sottogruppi di ![]() sono di questo tipo. Sia G un
sottogruppo di
sono di questo tipo. Sia G un
sottogruppo di ![]() .
Se
.
Se ![]() allora
allora
![]() .
Supponiamo che
.
Supponiamo che
![]() ,
allora l'insieme
,
allora l'insieme
![]() è non vuoto, in quanto
se
è non vuoto, in quanto
se ![]() è un elemento di G allora uno tra x e -x sta in S. Sia
è un elemento di G allora uno tra x e -x sta in S. Sia
![]() che esiste per l'assioma di buon ordinamento. Proviamo che allora
che esiste per l'assioma di buon ordinamento. Proviamo che allora
![]() .
Dato che
.
Dato che ![]() allora anche
allora anche ![]() per ogni
per ogni
![]() e quindi
e quindi
![]() .
Viceversa sia
.
Viceversa sia ![]() ,
allora esistono
,
allora esistono
![]() tali che g=nq+r con
tali che g=nq+r con ![]() .
Ora,
.
Ora,
![]() e quindi se fosse positivo contraddirebbe la minimalità di n, quindi
r=0, ossia g=nq, che vuol dire
e quindi se fosse positivo contraddirebbe la minimalità di n, quindi
r=0, ossia g=nq, che vuol dire
![]() .
.
![]()
Soluzione dell'esercizio 8.6 Dimostriamo la prima. Se n=0 è ovvia. Se n>O è immediato dalla definizione delle potenze
con esponente negativo. Se invece n<0 allora per definizione, si ha
(x-1)n=((x-1)-1)-n, e quindi per l'esercizio 8.2,
(x-1)n=x-n.
Dimostriamo la seconda per ![]() .
Procediamo per induzione su n.
Se n=0 allora
.
Procediamo per induzione su n.
Se n=0 allora
Se ora n<0 allora -n>0 e quindi, usando la definizione, la prima formula e
quanto abbiamo appena provato
La terza segue osservando che usando la seconda si ha:
Proviamo ora la quarta. Proviamolo per ![]() ,
procedendo per induzione su
m. Per m=0
,
procedendo per induzione su
m. Per m=0
Soluzione dell'esercizio 10.1 Sia
![]() ,
e sia
,
e sia
![]() la decomposizione in cicli
disgiunti. Sia
la decomposizione in cicli
disgiunti. Sia
![]() una trasposizione. Si hanno quattro possibilità:
una trasposizione. Si hanno quattro possibilità:
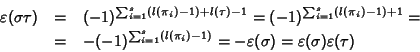
Caso (2).
Sia
![]() ,
allora
,
allora
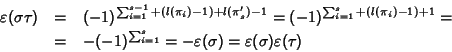
Case (3).
Sia
![]() allora
allora
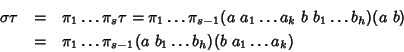
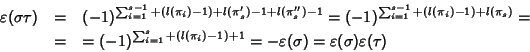
Caso (4).
Siano
![]() e
e
![]() .
Allora
.
Allora
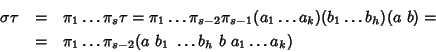
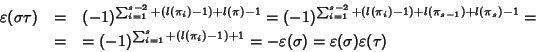
Soluzione dell'esercizio 14.1 Sono tutte verifiche elementari. Mostriamo, a titolo di esempio, che per la somma
e il prodotto di classi di resto vale la proprietà
distributiva
Mostriamo inoltre, con un esempio, che l'anello delle matrici non è
commutativo se ![]() .
Per n=2 si consideri il seguente esempio:
.
Per n=2 si consideri il seguente esempio:
Soluzione dell'esercizio 14.2 Tutte le asserzioni seguono da quanto visto nell'esercizio 8.1, tranne
la distributività. Proviamola. Siano
![]() e sia
e sia ![]() ,
allora
usando la distributività in R, si ha
,
allora
usando la distributività in R, si ha
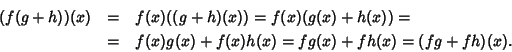
Soluzione dell'esercizio 14.3 Se
![]() è una unità, esiste
è una unità, esiste
![]() tale che
tale che
![]() ossia
ossia
![]() ,
che vuol dire
,
che vuol dire
![]() ,
e pertanto esiste y tale che ax-1=ny e quindi 1=ax-ny e quindi
per quanto osservato in 3.11, (a,n)=1.
,
e pertanto esiste y tale che ax-1=ny e quindi 1=ax-ny e quindi
per quanto osservato in 3.11, (a,n)=1.
Viceversa se (a,n)=1 esistono x,y tali che 1=ax+ny e quindi
![]() ,
ovvero
,
ovvero
![]() .
.
![]()
Soluzione dell'esercizio 14.4 Sia
![]() un divisore di zero. Se per assurdo (a,n)=1 allora per
l'esercizio precedente
un divisore di zero. Se per assurdo (a,n)=1 allora per
l'esercizio precedente
![]() sarebbe una unità , ma le unità non sono divisori di
zero.
sarebbe una unità , ma le unità non sono divisori di
zero.
Viceversa supponiamo che ![]() ,
allora
,
allora
![]() quindi
quindi
![]() .
D'altra parte
an/(n,m)=[n,m] è un multiplo di n e pertanto
.
D'altra parte
an/(n,m)=[n,m] è un multiplo di n e pertanto
![]() .
.
![]()
Soluzione dell'esercizio 14.5 In effetti il teorema precedente è un caso particolare dell'esercizio
8.4 in quanto le unità di un anello con identità R non sono
altro che gli elementi invertibili del monoide moltiplicativo ![]() .
.
![]()
Soluzione dell'esercizio 14.6 Segue immediatamente dagli esercizi 14.3 e 14.4
![]()
Soluzione dell'esercizio 14.7 Il gruppo delle unità di ![]() è
è ![]() e l'applicazione
e l'applicazione
![]() definita da
definita da
![]() e
e
![]() è un isomorfismo di gruppi.
è un isomorfismo di gruppi.
![]()
Soluzione dell'esercizio 15.1 Se R è commutativo, allora
(a+I)(b+I)=ab+I=ba+I=(b+I)(a+I) per ogni
![]() e quindi il quoziente è commutativo.
e quindi il quoziente è commutativo.
Se ![]() allora
(1+I)(a+I)=1a+I=a+I per ogni
allora
(1+I)(a+I)=1a+I=a+I per ogni ![]() e, analogamente
anche
(a+I)(1+I)=a+I per ogni a, quindi 1+I è l'identità del
quoziente. Dato che
e, analogamente
anche
(a+I)(1+I)=a+I per ogni a, quindi 1+I è l'identità del
quoziente. Dato che
![]() per definizione, la proiezione a quoziente
è un morfismo di anelli unitari.
per definizione, la proiezione a quoziente
è un morfismo di anelli unitari.
![]()
Soluzione dell'esercizio 15.2 Per l'analogo risultato per i gruppi si ha che
![]() è un sottogruppo per la somma.
è un sottogruppo per la somma.
Se ![]() e
e
![]() ,
allora
,
allora
![]() per ogni
per ogni ![]() ,
dato che
,
dato che ![]() è un ideale, allora
è un ideale, allora
![]() e
e
![]() per ogni
per ogni ![]() ,
quindi
,
quindi
![]() .
.
![]()
Soluzione dell'esercizio 15.3 Mimando la definizione di sottogruppo generato diremo che l'ideale generato da un sottoinsieme T dall'anello
R è il più piccolo ideale che contiene T, ossia se (T) è l'ideale
generato, allora
Soluzione dell'esercizio 15.4 Se se
![]() allora esiste
allora esiste ![]() tale che b=ac. Se I è un
ideale tale che
tale che b=ac. Se I è un
ideale tale che ![]() allora)d:di
allora)d:di
![]() e quindi
e quindi ![]() .
D'altra parte, proviamo che
.
D'altra parte, proviamo che
![]() è un ideale. Infatti se
è un ideale. Infatti se
![]() allora esistono
allora esistono
![]() tali che b1=ac1 e b2=ac2 e quindi
tali che b1=ac1 e b2=ac2 e quindi
![]() .
Se
.
Se ![]() e
e ![]() allora esiste
b=ca e quindi
allora esiste
b=ca e quindi
![]() .
.
![]()
Soluzione dell'esercizio 15.5 I+J è un ideale.
Siano
![]() allora esistono
allora esistono ![]() e
e ![]() tali che a=i+je a'=i'+j', ma allora
tali che a=i+je a'=i'+j', ma allora
![]() dato che,
essendo I e J degli ideali,
dato che,
essendo I e J degli ideali, ![]() e
e ![]() .
Sia
.
Sia ![]() ossia a=i+j con
ossia a=i+j con ![]() e
e ![]() .
Sia
.
Sia ![]() ,
allora
,
allora
![]() dato che,
essendo I e J degli ideali,
dato che,
essendo I e J degli ideali, ![]() e
e ![]() .
.
Osserviamo infine che se
![]() è un ideale che contiene sia I che
J, allora
è un ideale che contiene sia I che
J, allora ![]() per ogni
per ogni ![]() ei
ei ![]() per ogn
per ogn ![]() ,
poiché
H è un ideale,
,
poiché
H è un ideale, ![]() per ogni
per ogni ![]() e
e ![]() ,
quindi
,
quindi
![]() ,
da cui la tesi.
,
da cui la tesi.
![]()
Soluzione dell'esercizio 15.6 Sia ![]() una unità. Allora esiste
una unità. Allora esiste
![]() e quindi, usando la
2 della definizione di ideale,
e quindi, usando la
2 della definizione di ideale,
![]() .
Ma allora se
.
Ma allora se ![]() ,
usando
nuovamente la 2 della definizione di ideale
,
usando
nuovamente la 2 della definizione di ideale
![]() .
.
![]()
Soluzione dell'esercizio 15.7 In un corpo tutti gli elementi non nulli sono invertibili, quindi se I è
un ideale diverso da (0) allora I contiene un elemento invertibile. Per
l'esercizio precedente, I=R.
Viceversa sia
![]() si consideri (a) l'ideale generato da a ,
dato che
si consideri (a) l'ideale generato da a ,
dato che ![]() anche
anche ![]() e quindi (a)=R, ma allora
e quindi (a)=R, ma allora ![]() e
per l'esercizio 15.4 esiste
e
per l'esercizio 15.4 esiste ![]() tale che 1=ab e quindi a è invertibile.,
tale che 1=ab e quindi a è invertibile.,
![]()
Soluzione dell'esercizio 17.1 Dato che
![]() è un morfismo, si ha
è un morfismo, si ha
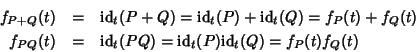
Soluzione dell'esercizio 18.1 Sia
![]() l'applicazione in questione, allora fP=0 se e solo se P(t)=0 per
ogni
l'applicazione in questione, allora fP=0 se e solo se P(t)=0 per
ogni ![]() .
Se K è infinito, per il principio di identità
dei polinomi,
questo implica che P=0.
.
Se K è infinito, per il principio di identità
dei polinomi,
questo implica che P=0.
D'altra parte se il campo è finito, allora
![]() .
Consideriamo allora il polinomio,
.
Consideriamo allora il polinomio,
![]() .
Chiaramente per ogni j si ha
.
Chiaramente per ogni j si ha
![]() e quindi fP=0, ovvero
e quindi fP=0, ovvero
![]() ,
da cui segue allora che
,
da cui segue allora che
![]() .
.
D'altra parte se
![]() allora
allora
![]() e quindi, per il
teorema di Ruffini,
e quindi, per il
teorema di Ruffini,
![]() .
.
![]() e quindi
e quindi
![]() e quindi
e quindi
![]() .
Per il
teorema di Ruffini allora
.
Per il
teorema di Ruffini allora
![]() e quindi
e quindi
![]() .
Procedendo per induzione, si prova allora che
.
Procedendo per induzione, si prova allora che
![]() ossia che
ossia che ![]() ,
ovvero
,
ovvero
![]() .
Mettendo insieme le due inclusioni si ha allora che
.
Mettendo insieme le due inclusioni si ha allora che
![]() .
.
![]()
Soluzione dell'esercizio 18.2 Osserviamo che mostrare la tesi equivale a mostrare che
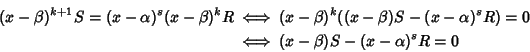
e l'ultima uguaglianza valutata in ![]() garantisce che
garantisce che
![]() e quindi
e quindi
![]() .
Per il teorema di Ruffini,
.
Per il teorema di Ruffini,
![]() e quindi
e quindi
![]() ,
e quindi la tesi.
,
e quindi la tesi.
![]()
Soluzione dell'esercizio 18.3 Sia
![]() e supponiamo che n non sia primo, esistono quindi
e supponiamo che n non sia primo, esistono quindi
![]() tali che 1<h,k<n e n=hk. Ma allora
n1=(hk)1=(h1)(k)1 e, dato che
tali che 1<h,k<n e n=hk. Ma allora
n1=(hk)1=(h1)(k)1 e, dato che
![]() ,
,
![]() e
e ![]() ,
questo contraddice il fatto che K,
essendo un campo, è un dominio di integrità.
,
questo contraddice il fatto che K,
essendo un campo, è un dominio di integrità.
![]()
Soluzione dell'esercizio 18.4 Per la proprietà distributiva si ha
pk= k(p1)=k0=0.
![]()
Soluzione dell'esercizio 22.1 Sia ![]() ,
allora per ogni
,
allora per ogni ![]() si ha
f2(x)=(f(x))2=f(x) e quindi
f2=f.
si ha
f2(x)=(f(x))2=f(x) e quindi
f2=f.
![]()
Soluzione dell'esercizio 22.2 Si consideri l'applicazione
![]() definita da
definita da
![]() essendo
essendo ![]() la funzione indicatrice di A, ossia
la funzione indicatrice di A, ossia
Soluzione dell'esercizio 22.3 Se ![]() allora r(r-1)=0, quindi se
allora r(r-1)=0, quindi se ![]() e
e ![]() si ha che r è
un divisore di zero e quindi non è invertibile, e quindi la tesi.
si ha che r è
un divisore di zero e quindi non è invertibile, e quindi la tesi.
![]()
Soluzione dell'esercizio 22.4 Basta fare tutte le verifiche. Diamo però un'altra dimostrazione. Osserviamo
che
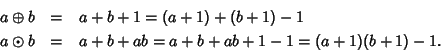
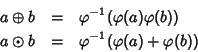
Soluzione dell'esercizio 23.3 Dalle definizioni di massimo comun divisore e di minimo comune multiplo segue immediatamente che (a,b) e [a,b] sono
rispettivamentel'estremo inferiore e l'estremo superiore di
![]() .
I relativi teoremi di esistenza (3.8 e 4.5)
permettono di concludere.
.
I relativi teoremi di esistenza (3.8 e 4.5)
permettono di concludere.
![]()
Soluzione dell'esercizio 23.4 (1). Se a e a' sono minimi, allora ![]() ,
dato che a è minimo, ma
anche
,
dato che a è minimo, ma
anche ![]() dato che a' è minimo. Ma allora per la
antisimmetria si ha che a=a'.
dato che a' è minimo. Ma allora per la
antisimmetria si ha che a=a'.
(2). Analoga alla precedente.
(3). Segue da (2), dato che l'estremo inferiore è il massimo dei minoranti.
(4). Segue da (1).
(5). Se è minimo è ovviamente minimale. In generale non è vero il
vicevers. Si consideri
![]() con l'ordinamento parziale indotto da
con l'ordinamento parziale indotto da
![]() ,
allora ogni primo è minimale, infatti se p è primo e
,
allora ogni primo è minimale, infatti se p è primo e
![]() allora n=1 o n=p, dato che
allora n=1 o n=p, dato che ![]() si ha che n=p.
si ha che n=p.
(6). L'esempio si ottiene prendendo lo stesso X del punto precedente con l'ordinamento inverso.
(7). Sia
![]() ,
e sia x un minorante di Y allora
,
e sia x un minorante di Y allora ![]() ,
dato che
,
dato che
![]() .
D'altra parte a è un minorante di Y, quindi è il massimo dei
minoranti di Y, ossia
.
D'altra parte a è un minorante di Y, quindi è il massimo dei
minoranti di Y, ossia ![]() .
In generale il viceversa non è vero. Si
pensi all'esempio dell'esercizio precedente,
.
In generale il viceversa non è vero. Si
pensi all'esempio dell'esercizio precedente, ![]() ordinato parzialmente da
ordinato parzialmente da
![]() ,
allora
,
allora
![]() ma
ma ![]() non ha minimo.
non ha minimo.
(8). Analogo al caso precedente. Come esempio si prenda ![]() ordinato parzialmente da
ordinato parzialmente da
![]() ,
allora
,
allora
![]() ma
ma ![]() non ha massimo.
non ha massimo.
![]()
Soluzione dell'esercizio 24.1 Se ![]() evidentemente x verifica le proprietà caratterizzanti
dell'estremo inferiore:
evidentemente x verifica le proprietà caratterizzanti
dell'estremo inferiore:
La seconda equivalenza segue dal principio di dualità dei reticoli, infatti,
la prima equivalenza, applicata al reticolo duale di ![]() dice che
dice che
Soluzione dell'esercizio 25.1 Supponiamo che ![]() ,
allora
,
allora
![]() ,
ma per la
proprietà di assorbimento si ha che
,
ma per la
proprietà di assorbimento si ha che
![]() e quindi
e quindi
![]() .
.
Viceversa, supponiamo che
![]() ,
allora, usando le proprietà commutativa e di assorbimento,
,
allora, usando le proprietà commutativa e di assorbimento,
![]() .
.
![]()
Soluzione dell'esercizio 25.2 Dimostiamo che
![]() .
Infatti
.
Infatti
|
|
= |
|
(ipotesi 1) |
| = |
|
(commutativa) | |
| = |
|
(assorbimento) | |
| = |
|
(ipotesi 1) | |
| = |
|
(commutativa) | |
| = |
|
(associativa) | |
| = |
|
(assorbimento) |
Soluzione dell'esercizio 27.2 Si mimi la dimostrazione dei teoremi di omomorfismo per
gruppi e per anelli.
![]()