


Next: Lezione 13 (3 aprile
Up: Matematica Discreta (II modulo)
Previous: Lezione 11 (29 marzo
Subsections
Il teorema cinese del resto
Teorema 12.1 (Cinese del resto)
Il sistema di congruenze
ha soluzione se e solo se
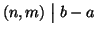
.
Se
c è una soluzione del sistema, allora gli elementi di
![$\left[c\right]_{[n,m]}$](img704.gif)
sono tutte e sole le soluzioni del sistema (i.e. le soluzioni sono
tutte e sole della forma
c+
k[
n,
m] al variare di
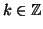
).
Dimostrazione.
Sia c una soluzione del sistema allora esistono
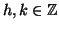 tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
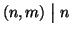 e
e
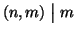 si ha che
si ha che
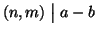 .
Viceversa, supponiamo che
.
Viceversa, supponiamo che
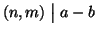 ,
allora esistono
,
allora esistono
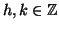 tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
Sia
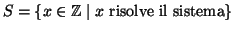 .
Dobbiamo provare
che se c è una soluzione allora
.
Dobbiamo provare
che se c è una soluzione allora
![$S=\left[c\right]_{[n,m]}$](img710.gif) .
.
![$S\subseteq\left[c\right]_{[n,m]}$](img711.gif) .
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
.
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
Ma allora
![$[n,m]\mathrel{\big\vert}c-c'$](img713.gif) ossia
ossia
![$c'\cong c\quad{\rm mod}\ [n,m]$](img714.gif) ovvero
ovvero
![$c'\in\left[c\right]_{[n,m]}$](img715.gif) .
.
![$\left[c\right]_{[n,m]}\subseteq S$](img716.gif) .
Sia
.
Sia
![$c'\in\left[c\right]_{[n,m]}$](img715.gif) ,
ovvero
c'=c+h[n,m]. Dal fatto che
,
ovvero
c'=c+h[n,m]. Dal fatto che
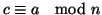 e che
e che
![$h[n,m]\cong 0\quad{\rm mod}\ n$](img718.gif) segue che
segue che
![$c'=c+h[n,m]\cong a \quad{\rm mod}\ n$](img719.gif) .
In modo analogo si ha che
.
In modo analogo si ha che
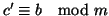 e
quindi che
e
quindi che 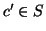 .
.

Esercizio 12.1
Siano
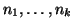
interi a due a due primi tra loro. Si provi che il
sistema di congruenze
ammette soluzione e che se
c è una soluzione, tutte le altre sono del tipo
![$c + k n_1\cdot\dots\cdot n_k]$](img724.gif)
.
Soluzione
Esercizio 12.2
Siano
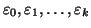
le cifre della espressione decimale del numero
n. Si provi che
- 1.
-
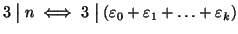
- 2.
-
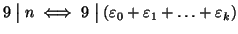
- 3.
-
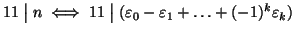
Soluzione
Elementi invertibili modulo n
Definizione 12.2
Sia
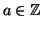
diremo che
a è
invertibile modulo n se esiste
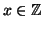
tale che

(in
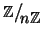
). Un tale
x si dice un
inverso di a modulo n.
Dimostrazione.
Se a è invertibile e x è un suo inverso, allora
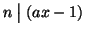 ,
quindi esiste k tale che nk=ax-1 e quindi 1=nk-ax, da cui 1=(a,n).
,
quindi esiste k tale che nk=ax-1 e quindi 1=nk-ax, da cui 1=(a,n).
Viceversa, se 1=(a,n) allora esistono
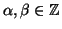 tali che
tali che
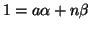 ,
ma allora
,
ma allora
 .
.

Dimostrazione. Dal fatto che ax=1 in
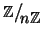 ,
moltiplicando entrambi i membri per y, ed usando
le proprietà associativa, commutativa e dell'1 si ottiene
,
moltiplicando entrambi i membri per y, ed usando
le proprietà associativa, commutativa e dell'1 si ottiene

Proposizione 12.5
Sia
a invertibile modulo
n e sia
a'=
a in
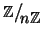
allora anche
a' è
invertibile e
a e
a' hanno gli stessi inversi.
Dimostrazione.
Se ax=i in
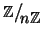 allora
allora
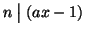 ,
se a'=a in
,
se a'=a in
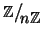 allora
esiste k tale che a'=a+kn. Ma allora
a'x-1=ax-1+knx è divisibile per ne quindi a'x=1 in
allora
esiste k tale che a'=a+kn. Ma allora
a'x-1=ax-1+knx è divisibile per ne quindi a'x=1 in
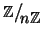 .
.

Osservazione 12.6
Osserviamo che le due proposizioni precedenti permettono di definire
l'invertibilità e l'inverso di una classe di congruenza. Diremo che
![$\left[a\right]_n$](img736.gif)
è invertibile se e solo se
a è invertibile modulo
n (
la
seconda delle proposizioni
assicura che tale definizione dipende solo dalla classe e non dal
rappresentante) e permette di d. Se
![$\left[a\right]$](img737.gif)
è invertibile, l'insieme
degli inversi di
a (che dipende solo dalla classe e non dal rappresentante)
formano una classe di congruenza, che viene chiamata l'
inverso di
![$\left[a\right]_n$](img736.gif)
e
denotata con
![$\left[a\right]_n^{-1}$](img738.gif)
.
La proposizione 12.3 può allora essere rienunciata
Dimostrazione.
Se 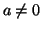 in
in
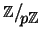 allora
allora
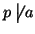 e quindi, dato che p è primo,
(p,a)=1, da cui la tesi.
e quindi, dato che p è primo,
(p,a)=1, da cui la tesi.




Next: Lezione 13 (3 aprile
Up: Matematica Discreta (II modulo)
Previous: Lezione 11 (29 marzo
Domenico Luminati
2001-06-18
![]() tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
![]() e
e
![]() si ha che
si ha che
![]() .
Viceversa, supponiamo che
.
Viceversa, supponiamo che
![]() ,
allora esistono
,
allora esistono
![]() tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
![]() .
Dobbiamo provare
che se c è una soluzione allora
.
Dobbiamo provare
che se c è una soluzione allora
![]() .
.
![]() .
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
.
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
![]() .
Sia
.
Sia
![]() ,
ovvero
c'=c+h[n,m]. Dal fatto che
,
ovvero
c'=c+h[n,m]. Dal fatto che
![]() e che
e che
![]() segue che
segue che
![]() .
In modo analogo si ha che
.
In modo analogo si ha che
![]() e
quindi che
e
quindi che ![]() .
.
![]()
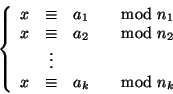
![]() ,
quindi esiste k tale che nk=ax-1 e quindi 1=nk-ax, da cui 1=(a,n).
,
quindi esiste k tale che nk=ax-1 e quindi 1=nk-ax, da cui 1=(a,n).
![]() tali che
tali che
![]() ,
ma allora
,
ma allora
![]() .
.
![]()
![]() ,
moltiplicando entrambi i membri per y, ed usando
le proprietà associativa, commutativa e dell'1 si ottiene
,
moltiplicando entrambi i membri per y, ed usando
le proprietà associativa, commutativa e dell'1 si ottiene
![]() allora
allora
![]() ,
se a'=a in
,
se a'=a in
![]() allora
esiste k tale che a'=a+kn. Ma allora
a'x-1=ax-1+knx è divisibile per ne quindi a'x=1 in
allora
esiste k tale che a'=a+kn. Ma allora
a'x-1=ax-1+knx è divisibile per ne quindi a'x=1 in
![]() .
.
![]()
![]() in
in
![]() allora
allora
![]() e quindi, dato che p è primo,
(p,a)=1, da cui la tesi.
e quindi, dato che p è primo,
(p,a)=1, da cui la tesi.
![]()