


Next: Lezione 14 (2 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 12 (2 aprile
Subsections
Equazioni lineari modulo n
Osservazione 13.1
Si osservi che se
a è invertibile in
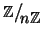
,
allora se
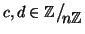
sono
tali che
ac=
ad (in
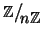
)
allora necessariamente
c=
d (in
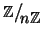
). In
quanto se
x è tale che
ax=1, allora
In particolare se
a è invertibile, allora da
ab= si deduce che
b=0.
In generale tale conclusione non si può inferire se
a non è invertibile,
ad esempio
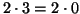
in
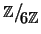
,
ma
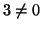
in
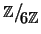
.
Se
p è primo
tutti gli elementi non nulli sono
invertibili, e quindi se
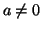
in
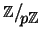
allora
ac=
ad in
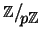
implica che
c=
d (in
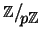
), in particolare
ab=0 in
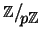
implica che
a=0 o
b=0.
Dimostrazione.
Se
 allora
allora
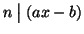 quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
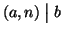 .
.
Viceversa supponiamo che
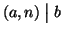 .
Siano
.
Siano
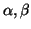 tali che
tali che
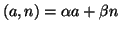 , e sia k tale che
b = k(a,n) allora
, e sia k tale che
b = k(a,n) allora
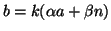 e quindi
e quindi
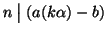 ,
ossia
,
ossia
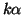 è una soluzione della congruenza.
è una soluzione della congruenza.

Osservazione 13.3
La dimostrazione precedente dà un metodo operativo per trovare una soluzione
della congruenza, basta usare l'algoritmo di Euclide per determinare
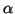
e
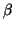
in modo che
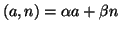
.
Esercizio 13.1
Si provi che quando ha soluzione, la congruenza

è
equivalente alla congruenza
essendo
a'=
a/(
a,
n),
b'=
b/(
a,
n),
n'=
n/(
a,
n). (Con equivalente si intende
che hanno le stesse soluzioni).
Soluzione
Proposizione 13.4
Siano
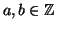
,
e sia
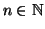
tale che (
a,
n)=1 allora l'insieme degli
x tali che

sono una classe di congruenza modulo
n.
Dimostrazione.
La congruenza ha soluzioni per quanto visto sopra. Passando alle classi di congruenza, si
ha che se x è una soluzione, allora
![$\left[a\right]_n\left[x\right]_n =\left[b\right]_n$](img759.gif) e
dato che a è invertibile, questo implica, moltiplicando entrambi membri
per
e
dato che a è invertibile, questo implica, moltiplicando entrambi membri
per
![$\left[a\right]_n^{-1}$](img738.gif) ,
che
,
che
![$\left[x\right]_n=\left[a\right]_n^{-1}\left[b\right]_n$](img760.gif) ,
da cui la
tesi.
,
da cui la
tesi.

Osservazione 13.5
La proposizione
13.4 e l'esercizio
13.1 forniscono un
metodo per trovare tutte le soluzioni di un'equazione lineare.
Il piccolo teorema di Fermat
Dimostrazione.
uv(v-1u-1)=u(vv-1)u-1=u1u-1=uu-1=1.

Osservazione 13.7
Una immediata conseguenza della proposizione precedente, è che se si fissa
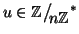
,
allora è possibile definire la funzione
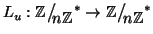
ponendo
Lu(
v)=
uv, e t. Per quanto osservato
sopra tale funzione risulta iniettiva, infatti
Lu(
v1)=
Lu(
v2) vuol dire che
uv1=
uv2, e dato che
u è invertibile,
v1=
v2. Dato che l'insieme
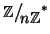
è finito,
Lu è bigettiva.
Dato un numnero naturale n si indica con 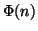 il numero di naturali
minori o uguali a n e coprimi con n. La funzione
il numero di naturali
minori o uguali a n e coprimi con n. La funzione 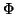 si chiama
funzione
si chiama
funzione 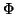 di Eulero. La seguente proposizione è una conseguenza
immediata di proposizione 12.3 e di proposizione 11.13.
di Eulero. La seguente proposizione è una conseguenza
immediata di proposizione 12.3 e di proposizione 11.13.
Proposizione 13.8
Per ogni
n>0, si ha che
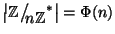
.
Dimostrazione.
Sia 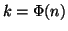 ,
e siano
,
e siano
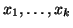 tutti gli elementi di
tutti gli elementi di
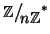 ,
dato
che l'applicazione Lu è bigettiva, allora
,
dato
che l'applicazione Lu è bigettiva, allora
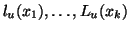 sono
ancora tutti gli elementi di
sono
ancora tutti gli elementi di
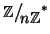 ,
ma allora, per la commutatività del
prodotto,
,
ma allora, per la commutatività del
prodotto,
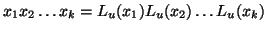 e quindi
e quindi
Da, questa uguaglianza, osservando che
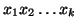 è
invertibile, ne
segue che
uk=1.
è
invertibile, ne
segue che
uk=1.

Corollario 13.10 (Piccolo teorema di Fermat)
Se
p è un primo allora per ogni
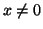
in
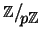
si ha che
xp-1=1 in
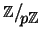
.
Dimostrazione.
Segue immediatamente dal teorema precedente, osservando che se p è primo,
allora tutti i numeri più piccoli di p sono coprimi con p, e quindi
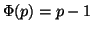 .
.

Esercizio 13.2
Si provi che se
p è un primo allora per ogni intero
x si ha che
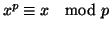
.
Soluzione
Crittografia RSA
Proposizione 13.11
Sia
c coprimo con
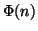
,
allora l'applicazione
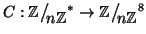
definita da
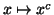
è invertibile e la sua inversa è data da
D(
x)=
xd essendo
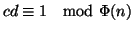
.
Dimostrazione.
Se c è coprimo con 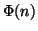 allora esiste un d come nell'enunciato, ossia
tale che
allora esiste un d come nell'enunciato, ossia
tale che
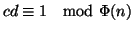 ,
ma allora
,
ma allora
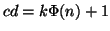 e quindi, usando
la proposizione dimostrata precedentemente, per ogni
e quindi, usando
la proposizione dimostrata precedentemente, per ogni
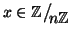 si ha
si ha
Del tutto analoga è la prova che anche C(D(x))=x per ogni x, da cui la
tesi.

La proposizione appena dimostrarta è alla base del metodo RSA di
crittografia a chiave pubblica. Supponiamo cha A debba trasmettere un
messaggio riservato a B, allora B rende noti due numeri m e c (detti
rispettivamente il modulo e la chiave di codifica), che hanno la proprietà
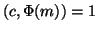 .
L'alfabeto della trasmissione sarà allora costituito da
.
L'alfabeto della trasmissione sarà allora costituito da
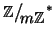 e la codifica sarà costituita da sostituire la lettera x con
xc (modulo m).
e la codifica sarà costituita da sostituire la lettera x con
xc (modulo m).
Il fatto che
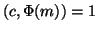 ,
garantisce che si può determinare un numero dtale che
,
garantisce che si può determinare un numero dtale che
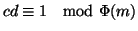 ,
ossia tale che
,
ossia tale che
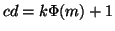 .
Per
decodificare il messagio è allora sufficiente elevare alla potenza d, in
quanto
.
Per
decodificare il messagio è allora sufficiente elevare alla potenza d, in
quanto
Chiaramente chiunque conosca c e 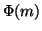 è in grado di determinare la
chiave di decodifica d. Ma determinare
è in grado di determinare la
chiave di decodifica d. Ma determinare 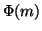 è molto facile se si
conosce la fattorizzazione in primi di m, e fattorizzare un intero è un
problema computazionalmente molto complesso. Quindi soltanto chi ha costruito
m e c è in grado di determinare d facilmente. I numeri che vengono usati
sono in realtà del tipo m=pq con p,q primi, per i quali si
ha
è molto facile se si
conosce la fattorizzazione in primi di m, e fattorizzare un intero è un
problema computazionalmente molto complesso. Quindi soltanto chi ha costruito
m e c è in grado di determinare d facilmente. I numeri che vengono usati
sono in realtà del tipo m=pq con p,q primi, per i quali si
ha
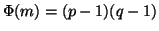 e per i quali,
determinare
e per i quali,
determinare 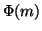 a partire da m è equivalente a determinare la fattorizzazione di m.
a partire da m è equivalente a determinare la fattorizzazione di m.
Esercizio 13.3
Provare che se
p,
q sono primi allora
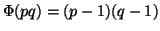 Soluzione
Soluzione
Esercizio 13.4
Supponiamo che
n=
pq sia con
p e
q primi. Si provi che se si conoscono
n e
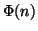
si possono determinare
pe
q.
Soluzione



Next: Lezione 14 (2 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 12 (2 aprile
Domenico Luminati
2001-06-18
![]() allora
allora
![]() quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
![]() .
.
![]() .
Siano
.
Siano
![]() tali che
tali che
![]() , e sia k tale che
b = k(a,n) allora
, e sia k tale che
b = k(a,n) allora
![]() e quindi
e quindi
![]() ,
ossia
,
ossia
![]() è una soluzione della congruenza.
è una soluzione della congruenza.
![]()
![]() e
dato che a è invertibile, questo implica, moltiplicando entrambi membri
per
e
dato che a è invertibile, questo implica, moltiplicando entrambi membri
per
![]() ,
che
,
che
![]() ,
da cui la
tesi.
,
da cui la
tesi.
![]()
![]()
![]() il numero di naturali
minori o uguali a n e coprimi con n. La funzione
il numero di naturali
minori o uguali a n e coprimi con n. La funzione ![]() si chiama
funzione
si chiama
funzione ![]() di Eulero. La seguente proposizione è una conseguenza
immediata di proposizione 12.3 e di proposizione 11.13.
di Eulero. La seguente proposizione è una conseguenza
immediata di proposizione 12.3 e di proposizione 11.13.
![]() ,
e siano
,
e siano
![]() tutti gli elementi di
tutti gli elementi di
![]() ,
dato
che l'applicazione Lu è bigettiva, allora
,
dato
che l'applicazione Lu è bigettiva, allora
![]() sono
ancora tutti gli elementi di
sono
ancora tutti gli elementi di
![]() ,
ma allora, per la commutatività del
prodotto,
,
ma allora, per la commutatività del
prodotto,
![]() e quindi
e quindi
![]() .
.
![]()
![]() allora esiste un d come nell'enunciato, ossia
tale che
allora esiste un d come nell'enunciato, ossia
tale che
![]() ,
ma allora
,
ma allora
![]() e quindi, usando
la proposizione dimostrata precedentemente, per ogni
e quindi, usando
la proposizione dimostrata precedentemente, per ogni
![]() si ha
si ha
![]() .
L'alfabeto della trasmissione sarà allora costituito da
.
L'alfabeto della trasmissione sarà allora costituito da
![]() e la codifica sarà costituita da sostituire la lettera x con
xc (modulo m).
e la codifica sarà costituita da sostituire la lettera x con
xc (modulo m).
![]() ,
garantisce che si può determinare un numero dtale che
,
garantisce che si può determinare un numero dtale che
![]() ,
ossia tale che
,
ossia tale che
![]() .
Per
decodificare il messagio è allora sufficiente elevare alla potenza d, in
quanto
.
Per
decodificare il messagio è allora sufficiente elevare alla potenza d, in
quanto