Soluzione di alcuni degli esercizi proposti

Soluzione dell'esercizio 1.1  

    

Soluzione dell'esercizio 1.2  

    

Soluzione dell'esercizio 1.3  

    

Soluzione dell'esercizio 1.4  

    

Soluzione dell'esercizio 1.5  

    

Soluzione dell'esercizio 1.6  

    

Soluzione dell'esercizio 1.7  

    

Soluzione dell'esercizio 1.8  

    

Soluzione dell'esercizio 1.9  

    

Soluzione dell'esercizio 2.1  

    

Soluzione dell'esercizio 2.2  

    

Soluzione dell'esercizio 2.3  

    

Soluzione dell'esercizio 2.4  

    

Soluzione dell'esercizio 2.5  

    

Soluzione dell'esercizio 3.1  

    

Soluzione dell'esercizio 3.2  Proviamo soltanto l'associatività della somma. Dobbiamo provare che per ogni $n,m,k\in\mathbb N$ si ha che (n+m)+k=n+(m+k). Procediamo per induzione su k. Se k=0 dalla definizione si ha (n+m)+ 0 =n+m e anche n+(m+0)=n+(m)=n+m. Supponiamo la tesi vera per k e proviamola per $\mathop{\rm succ}\nolimits(k)$.

$$\begin{eqnarray*}(m+n)+\mathop{\rm succ}\nolimits(k) & = & \mathop{\rm succ}\nol... ...thop{\rm succ}\nolimits(n+k)=m+(n+\mathop{\rm succ}\nolimits(k)) \end{eqnarray*}$$

    

Soluzione dell'esercizio 3.3  

    

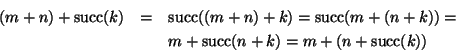
Soluzione dell'esercizio 4.2  Siano $f:X\to I_n$ e $g:Y\to I_n$ due bigezioni, allora l'applicazione $h:I_{n+m}\to X\cup Y$ definita da

$$h(i)=\Big\langle \begin{array}{lcl} f(i) &&\hbox{\rm {se }} i<n \\ g(i-n) && \hbox{\rm {se }} n\le i < m+n \end{array}$$

è una bigezione.

Per la seconda parte si osservi innanzitutto che $X= (X-Y)\cup (X\cap Y)$ e che $(X-Y)\cap (X\cap Y)=\varnothing$ e che quindi per l'esercizio precedente,

$$\left\vert X\right\vert = \left\vert X-Y\right\vert + \left\vert X\cap Y\right\vert$$

osserviamo inoltre che $X\cup Y=(X-Y)\cup Y$ con $(X-Y)\cap Y=\varnothing$e quindi $\left\vert X\cup Y\right\vert= \left\vert X-Y\right\vert+ \left\vert Y\right\vert$, da cui

$$\left\vert Y\right\vert=\left\vert X\cup Y\right\vert - \left\vert X-Y\right\vert$$

sommando queste due relazioni si ottiene la tesi.     

Soluzione dell'esercizio 4.3  Procediamo per induzione su n. Se n=1 non c'è nulla da dimostrare. Supponiamo la tesi vera per n, usando l'associatività dell'unione si ha

$$\bigcup_{i=1}^{n+1} X_i= ( \bigcup_{i=1}^{n} X_i )\cup X_{n+1}$$

e dato che gli X_i sono a due a due disgiunti, anche $( \bigcup_{i=1}^{n} X_i )\cap X_{n+1}=\varnothing$, ma allora per l'esercizio precedente, e l'ipotesi di induzione, si ha che

$$\left\vert\bigcup_{i=1}^{n+1} X_i\right\vert= \left\vert\big... ...t X_{n+1}\right\vert=\sum_{i+1}^{n+1}\left\vert X_i\right\vert$$

    

Soluzione dell'esercizio 4.4  

    

Soluzione dell'esercizio 4.5  

    

Soluzione dell'esercizio 4.6  

    

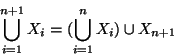
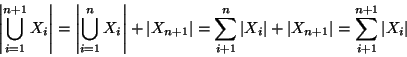
Soluzione dell'esercizio 5.1   Se una tale g esiste, f è surgettiva, dato che per ogni $y\in Y$si ha che f(g(y))=y.

Viceversa, supponiamo che f sia surgettiva, allora $f^{-1}(y)\ne\varnothing$ per ogni $y\in Y$, per l'assioma di scelta, esiste una funzione di scelta, $g:Y\to\bigcup_{y\in Y}f^{-1}(y)$, tale che $g(y)\in f^{-1}(y)$ per ogni $y\in Y$, ma ciò significa che f(g(y))=y per ogni $y\in Y$, ossia che g è una inversa destra di f.     

Soluzione dell'esercizio 5.2  Se una tale g esiste allora f deve necessariamente essere iniettiva, infatti se f(x₁)=f(x₂) allora x₁=g(f(x₁))=g(f(x₂))x₂.

Viceversa, supponiamo che f sia iniettiva. Allora per ogni $y\in f(X)$ esiste un unico $x_y\in X$ tale che f(x_y)=y. Preso un arbitrario $\overline{x}\in X$definiamo $g:Y\to X$ ponendo

$$g(y)=\Big\langle \begin{array}{lcl} x_y &&\hbox{\rm {se }}y... ...) \\ \overline{x} &&\hbox{\rm {se }}y\notin f(X) \end{array}$$

Dato che per ogni $x\in X$ l'unico elemento avente f(x) come immagine è x stesso, si ha che g(f(x))=x.     

Soluzione dell'esercizio 5.3  

    

Soluzione dell'esercizio 6.1  

    

Soluzione dell'esercizio 6.2  A partire dagli X_m costruiamo dei nuovi insiemi, ponendo

$$\begin{eqnarray*}Y_0 & = & X_0 \\ Y_{n+1} & = & X_{n+1} - \bigcup_{m=0}^{n} X_m \qquad \forall n \ge 0 \end{eqnarray*}$$

Gli insiemi in questione sono a due a due disgiunti, e $\bigcup_nY_n=\bigcup_nX_n$. Si consideri l'insieme $A=\{n\in\mathbb N\mid Y_n\ne\varnothing\}$, allora $Y=\bigcup_{n\in A}Y_n$. Per quanto visto in precedenza Aè finito o numerabile. Nel primo caso A è finito, nel secondo caso è numerabile.     

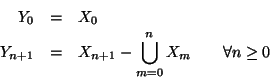
Soluzione dell'esercizio 6.3  Come nell'esercizio precedente, poniamo

$$\begin{eqnarray*}Y_0 & = & X_0 \\ Y_{n+1} & = & X_{n+1} - \bigcup_{m=0}^{n} X_m \qquad \forall n \ge 0 \end{eqnarray*}$$

Gli insiemi in questione sono a due a due disgiunti, e $\bigcup_nY_n=\bigcup_nX_n$. Si consideri l'insieme $A=\{n\in\mathbb N\mid \left\vert Y_n\right\vert=\aleph_0\}$, $B=\{n\in\mathbb N\mid Y_n\ne\varnothing\hbox{\rm { ed \\lq e finito}}\}$, allora $Y=\bigcup_{n\in A}Y_n\cup\bigcup_{n\in B}Y_n$. Per quanto visto in precedenza A, e B sono finiti o numerabili. Dato che Y₀ è numerabile, $A\ne\varnothing$e quindi $\bigcup_{n\in A}Y_n$ è numerabile. D'altra parte $\bigcup_{n\in B}Y_n$ è finito o numerabile e quindi la loro unione è numerabile.     

Soluzione dell'esercizio 6.4  

    

Soluzione dell'esercizio 6.5  

    

Soluzione dell'esercizio 6.6  

    

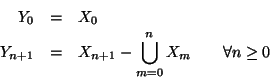
Soluzione dell'esercizio 6.7  La funzione $f:(0,1)\to\mathbb R$ definita da $f(t)=\tan(\pi t-\pi/2)$ è una bigezione.     

Soluzione dell'esercizio 6.8  Osserviamo che X-Y non può essere né finito né numerabile, altrimenti $X=(X-Y)\cup Y$ sarebbe numerabile. Ma allora X-Ycontiene un sottinsieme, Y', numerabile. Dato che Y e Y' sono entrambi numerabili, la loro unione è numerabile, sia quindi $f:Y'\to Y\cup Y'$ una bigezione e si definisca $g:X-Y\to X$ ponendo:

$$g(x)=\Big\langle \begin{array}{lcl} f(x) &&\hbox{\rm {se }} x\in Y' \\ x &&\hbox{\rm {se }} x\in X-(Y\cup Y') \end{array}$$

g è chiaramente una bigezione.     

Soluzione dell'esercizio 6.9  Per ogni $k\in \mathbb N$ sia $F_k=\{A\in 2^\mathbb N\mid \left\vert A\right\vert = k\}$. Chiaramente $F=\bigcup_{k\in\mathbb N}F_k$. Proviamo che $\left\vert F_k\right\vert=\aleph_0$ per ogni $k\ge 1$. Procediamo per induzione su k. Se k=1 allora l'applicazione $n\to \{n\}$è una bigezione $\mathbb N\to F_1$. Supponiamo che F_k sia numerabile, allora per ogni $A\in F_k$ sia $F_{k+1}(A)=\{B\in F_{k+1}\mid B\supseteq A\}$. per ogni Al'insieme F_k+1(A) è numerabile, in quanto in bigezione con $\mathbb N-A$, inoltre $F_{k+1}-\bigcup_{A\in F_k}F_{k+1}(A)$ è numerabile in quanto unione di una famiglia numerabile di insiemi numerabili.     

Soluzione dell'esercizio 6.10  

    

Soluzione dell'esercizio 7.1  

    

Soluzione dell'esercizio 7.2  

    

Soluzione dell'esercizio 7.3  

    

Soluzione dell'esercizio 7.4  

    

Soluzione dell'esercizio 8.1  Dalla definizione del coefficiente binomiale si ha

$${n \choose k}+{n \choose k-1} = \frac{n!}{k!(n-k)!}+\frac{n!... ...)!(n-k+1)!} = \frac{n!(n+1)}{(k)!(n-k+1)!} = {n+1 \choose k}$$

    

Soluzione dell'esercizio 8.2  Si osservi che se X è un insieme con n elementi, allora

$$2^X=\bigcup_{i=0}^n{X \choose k}$$

e che questi insiemi sono a due a due disgiunti. Quindi

$$2^n=2^{\left\vert X\right\vert}=\left\vert 2^X\right\vert=\su... ...n{\left\vert X\right\vert \choose k}=\sum_{i=0}^n{n \choose k}$$

    

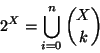
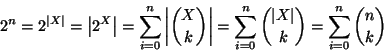
Soluzione dell'esercizio 10.1  Procediamo per induzione su k. Se k=1 non c'è nulla da dimostrare. Supponiamo che la tesi sia vera per k e supponiamo che $p\mathrel{\big\vert}n_1n_2\dots n_{k+1}$, ossia $p\mathrel{\big\vert}(n_1n_2\dots n_k)n_{k+1}$. Per il corollario 10.2, si ha che $p\mathrel{\big\vert} n_1n_2\dots n_k$ oppure $p\mathrel{\big\vert}n_{k+1}$. Se si verifica la seconda eventualità abbiamo finito, altrimenti, per ipotesi di induzione esiste $i\in \{1,\dots,k\}$ tale che $p\mathrel{\big\vert}n_i$, e quindi si conclude.     

Soluzione dell'esercizio 10.2  

    

Soluzione dell'esercizio 10.3  

    

Soluzione dell'esercizio 10.4  Chiaramente $\prod _{i=1}^s p_i^{k_i\wedge h_i}$ è un divisore comune a n e m. Inoltre se c è un divisore comune non può avere fattori primi diversi dai p_i, quindi $c=\prod _{i=1}^s p_i^{l_i}$. Dal fatto che $c\mathrel{\big\vert}n$ segue allora che $l_i\le k_i$ e dal fatto che $c\mathrel{\big\vert}m$ segue che $l_i\le h_i$ per ogni i, e quindi $l_i\le k_i\wedge h_i$.

La formula per il m.c.m. segue allora dal fatto che $[n,m]=\left\vert nm\right\vert/(n,m)$, e che per ogni coppia di numeri reali si ha che $h+k-h\wedge k=h\vee k$.     

Soluzione dell'esercizio 11.1  

    

Soluzione dell'esercizio 12.1  

    

Soluzione dell'esercizio 12.2  

    

Soluzione dell'esercizio 13.1  

    

Soluzione dell'esercizio 13.2  

    

Soluzione dell'esercizio 13.3  Osserviamo che $(a,pq)\ne1$ se e solo se $p \mathrel{\big\vert}a$ o $p \mathrel{\big\vert}a$, ma i numeri più piccoli di pq che sono divisibili per p sono p, $2p,\dots,qp$, quelli che sono divisibili per q sono invece q, $2q,\dots,pq$ e quindi i numeri più piccoli di pq e non coprimi con pq sono p+q-1. Quindi $\Phi(pq)=pq-(p+q-1)=(p-1)(q-1)$.     

Soluzione dell'esercizio 13.4   $\Phi(n)=(p-1)(q-1)=pq -p -q +1= n -p -q +1$ da cui $p+q=n+1-\Phi(n)$. Quindi p e q sono determinati dal sistema di equazioni

$$\left\{ \begin{array}{l} p+q=n+1-\Phi(n) \\ pq=n \end{array} \right.$$

Una semplice sostituzione mostra che allora p e q devono essere le due radici dell'equazione $x^2-(n+1-\Phi(n))+n=0$.     

Soluzione dell'esercizio 13.5  

    

Soluzione dell'esercizio 14.1  

    

Soluzione dell'esercizio 14.2  

    

Soluzione dell'esercizio 14.3  

    

Soluzione dell'esercizio 14.4  

    

Soluzione dell'esercizio 14.5  

    

Soluzione dell'esercizio 14.6  

    

Soluzione dell'esercizio 14.7  

    

Soluzione dell'esercizio 14.8  

    

Soluzione dell'esercizio 14.9  La colorazione dei lati data in figura 11

  

Figure 11: Soluzione grafica dell'esercizio 14.9

suggerisce come definire l'isomorfismo. Precismante se si definisce la funzione $f:\{1,2,\dots,10\}\to\{a,b,\dots,j\}$ ponendo

$$\begin{array}{rclcrclcrclcrclcrcl} f(1)&=&a &\quad & f(2)&=&... ...d & f(8)&=&h &\quad & f(9)&=&i &\quad & f(10)&=&j \end{array}$$

una semplice verifica mostra che f è un isomorfismo.     

Soluzione dell'esercizio 14.10  

    

Soluzione dell'esercizio 14.11  

    

Soluzione dell'esercizio 14.12  Se identifichiamo la lettera a con il numero 0 e la b con l'1, si ottiene una identificazione delle parole con le coordinate dei vertici del cubo di $\mathbb R^3$ dato da $[0,1]\times[0,1]\times[0,1]$. Inoltre due vertici di tale cubo sono congiunti da uno spigolo se solo se differiscono esattamente per una coordinata. L'identificazione data è quindi un isomorfismo di grafi tra G e G'.

  

Figure 12: L'isomorfismo tra i grafi dell'esercizio 14.12

    

Soluzione dell'esercizio 16.1  La prima segue dal fatto che i vertici delle componenti connesse sono le classi d'equivalenza di una relazione d'equivalenza. La seconda, segue dal fatto che ogni lato di G deve essere lato di una qualche classe d'equivalenza, dato che i suoi estremi sono congiungibili e pertanto appartengono alla stessa classe d'equivalenza.     

Soluzione dell'esercizio 19.1  

    

Soluzione dell'esercizio 19.2  

    

Soluzione dell'esercizio 19.3  

    

Soluzione dell'esercizio 19.4  

    

Soluzione dell'esercizio 19.5  

    

Soluzione dell'esercizio 19.6  

    

Soluzione dell'esercizio 19.7  

    

Soluzione dell'esercizio 20.1  

    

Soluzione dell'esercizio 20.3  

    

Soluzione dell'esercizio 20.4  

    

Soluzione dell'esercizio 20.5  

    

Soluzione dell'esercizio 20.6  Siano $T_1,\dots,T_k$ le componenti connesse di F, allora ogni T_i è un albero, ma allora per ogni i si ha $\left\vert(\right\vert V(T_i))=\left\vert(\right\vert E(T_i))+1$. Dal fatto che $\sum_{i=1}^k\left\vert(\right\vert V(T_i)=\left\vert(\right\vert V)$ e $\sum_{i=1}^k\left\vert(\right\vert E(T_i)=\left\vert(\right\vert E)$segue immediatamente la tesi.     

Soluzione dell'esercizio 20.7  Sia T un albero generatore di G. Chiaramente $\left\vert V(T)\right\vert=\left\vert V(G)\right\vert$ e dato che T è un sottografo di G allora $\left\vert E(T)\right\vert\le \left\vert E(G)\right\vert$ e quindi, usando la formula che lega il numero di lati con il numero dei vertici di un grafo, si ha

$$\left\vert E(G)\right\vert\ge \left\vert E(T)\right\vert = \left\vert V(T)\right\vert - 1 = \left\vert V(G)\right\vert - 1.$$

    

Soluzione dell'esercizio 21.1