


Next: Lezione 4 (7 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 2 (28 febbraio
Subsections
Le operazioni sui naturali
Il teorema di ricorsione permette di definire la somma il prodotto di numeri
naturali.
Definizione 3.1
Dato
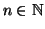
si definisce ;la funzione
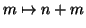
ricorsivamente nel
seguente modo:
ed analogamente si definisce il prodotto
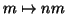
:
Osservazione 3.2
Se si chiamo 1=
succ(0), allora per ogni
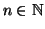
si ha che
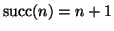
,
infatti dalla definizione di + si ha che
D'ora in poi non scriveremo più
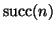
ma
n+1.
Esercizio 3.1
Si provi che per ogni
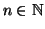
si ha 0+
n=
n e 1+
n=
n+1 ossia
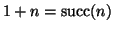
.
Soluzione
Esercizio 3.2
Si provino le usuali proprietà (i.e. associativa, commutativa, distributiva)
della somma e del prodotto di numeri naturali.
Soluzione
L'ordinamento dei naturali
Con la somma si può definire la nozione di ordinamento dei numeri naturali.
Osservazione 3.4
Si può vedere
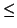
come un sottinsieme di
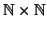
e precisamente
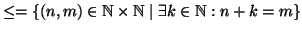
.
E quindi
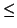
è una
relazione sui
naturali e quello che abbiamo definito come significato di
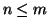
è
effettivamente lo stesso che dire
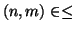
.
Si può dimostrare la seguente
Dimostrazione.
La dimostrazione è lasciata per esercizio agli studenti volonterosi. I punti
che richiedono maggiore attenzione sono il secondo e il quarto.

Insiemi ordinati
Definizione 3.6
Sia
X un insieme e
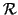
una relazione binaria su
X,
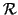
si dice
un
ordinamento parziale o anche una
relazione d'ordine parziale
se valgono le seguenti proprietà:
- 1.
- proprietà riflessiva:
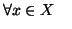
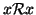 .
.
- 2.
- proprietà antisimmetrica:
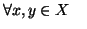
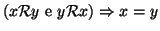
- 3.
- proprietà transitiva:
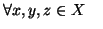
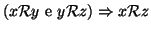
Un ordinamento parziale si dice un
ordinamento totale se in più vale
la
- 1.
- tricotomia:
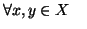
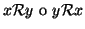 .
.
Una coppia
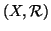
in cui
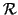
è un ordinamento (parziale o totale) si
dice un
insieme (parzialmente o totalmente) ordinato.
Osservazione 3.7
In genere le relazioni d'ordine si indicano con simboli del tipo
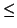
o
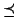
,
in tal caso quando si scriverà
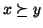
si intenderà
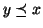
,
e quando si scriverà
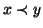
si intenderà il cosiddetto
ordinamento stretto ovvero
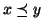
e
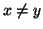
.
In termini
dell'ordinamento stretto la proprietà di tricotomia per l'ordinamento
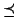
si può rioenunciare dicendo:
-
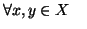 vale una e una sola delle tre seguenti:
vale una e una sola delle tre seguenti: 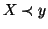 ,
x=y,
,
x=y, 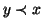 .
.
Osservazione 3.8
In termini di questo nuovo linguaggio
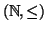
risulta quindi essere un
insieme totalmente ordinato.
Si possono dimostrare anche le ulteriori proprietche legano l'ordinamento con
le operazioni:
Dimostrazione.
Esercizio per lo studente volenteroso.

Insiemi finiti: il Lemma dei cassetti
Dato un numero naturale
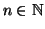 denotiamo con In l'insieme
denotiamo con In l'insieme
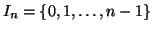 .
.
Definizione 3.10
Diremo che un insieme è
finito se esiste
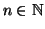
tale che
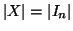
.
Un insieme è detto
infinito se non è finito
Teorema 3.11 (Lemma dei cassetti)
Siano
X e
Y due insiemi aventi rispettivamente
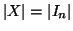
e
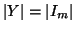
con
n<
m allora ogni applicazione
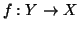
non è
iniettiva.
Dimostrazione.
Procediamo per induzione su n. Se n=0 allora
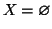 e
e
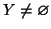 ,
quindi l'insieme XY delle applicazioni
,
quindi l'insieme XY delle applicazioni 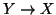 è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
Supponiamo che la tesi sia vera per n e proviamola per n+1. Sia
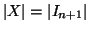 e sia,
e sia,
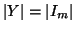 con m>n+1 e supponiamo per
assurdo che l'applicazione
con m>n+1 e supponiamo per
assurdo che l'applicazione 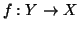 sia iniettiva. Per definizione esiste una
bigezione
sia iniettiva. Per definizione esiste una
bigezione
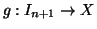 ;
poniamo xn=g(n) e
;
poniamo xn=g(n) e
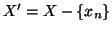 .
Chiaramente
X' è in bigezione con In. Si hanno due casi:
.
Chiaramente
X' è in bigezione con In. Si hanno due casi:
- 1.
-
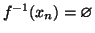 (i.e.
(i.e.
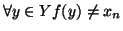 )
)
- 2.
-
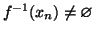 (i.e.
(i.e.
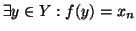 )
)
Nel primo caso,
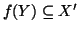 e quindi
e quindi 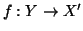 sarebbe un'applicazione
iniettiva da un insieme equipotente a Im in un insieme equipotente a In;
dato che m>n+1>n questo è assurdo per ipotesi di induzione.
sarebbe un'applicazione
iniettiva da un insieme equipotente a Im in un insieme equipotente a In;
dato che m>n+1>n questo è assurdo per ipotesi di induzione.
Nel secondo caso, sia  tale che f(y)=xn e sia
tale che f(y)=xn e sia
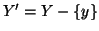 .
Dato che
f è iniettiva,
.
Dato che
f è iniettiva,
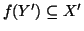 e quindi,
e quindi,
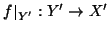 è una applicazione iniettiva. Dato che
è una applicazione iniettiva. Dato che
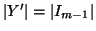 ,
,
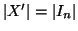 e m-1>n, ciò è assurdo per ipotesi di induzione.
e m-1>n, ciò è assurdo per ipotesi di induzione.

Osservazione 3.12
Il nome lemma dei cassetti deriva dal seguente modo naif di enunciare il
teorema precedente: se ho un certo numero di oggetti da sistemare in dei
cassetti, e il numero di oggetti è superiore a quello dei cassetti, almeno
un cassetto conterrà più di un oggetto.



Next: Lezione 4 (7 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 2 (28 febbraio
Domenico Luminati
2001-06-18
![]()
![]()
![]() e
e
![]() ,
quindi l'insieme XY delle applicazioni
,
quindi l'insieme XY delle applicazioni ![]() è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
è vuoto, e quindi non c'è
nulla da dimostrare (dal falso segue ogni cosa).
![]() e sia,
e sia,
![]() con m>n+1 e supponiamo per
assurdo che l'applicazione
con m>n+1 e supponiamo per
assurdo che l'applicazione ![]() sia iniettiva. Per definizione esiste una
bigezione
sia iniettiva. Per definizione esiste una
bigezione
![]() ;
poniamo xn=g(n) e
;
poniamo xn=g(n) e
![]() .
Chiaramente
X' è in bigezione con In. Si hanno due casi:
.
Chiaramente
X' è in bigezione con In. Si hanno due casi:
![]() tale che f(y)=xn e sia
tale che f(y)=xn e sia
![]() .
Dato che
f è iniettiva,
.
Dato che
f è iniettiva,
![]() e quindi,
e quindi,
![]() è una applicazione iniettiva. Dato che
è una applicazione iniettiva. Dato che
![]() ,
,
![]() e m-1>n, ciò è assurdo per ipotesi di induzione.
e m-1>n, ciò è assurdo per ipotesi di induzione.
![]()