


Next: Lezione 5 (12 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 3 (5 marzo
Subsections
Cardinalità degli insiemi finiti
Una prima immediata conseguenza del lemma dei cassetti è il seguente corollario:
Corollario 4.1
Se
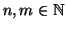
sono due naturali diversi
X e
Y sono insiemi finiti con
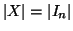
e
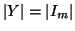
,
allora
X e
Y non sono
equipotenti.
In particolare, se
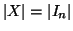
e
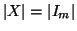
allora
n=
m.
Questo corollario fa sì che si possa definire la cardinalità degli insiemi
finiti.
Definizione 4.2
Sia
X un insieme finito, si dice
cardinalità di
X l'unico numero
naturale
n tale che
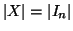
.
Tale numero si denota allora con
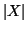
.
È facile provare la seguente
Proposizione 4.3
Due insiemi finiti sono equipotenti se e solo se
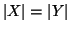
.
Dimostrazione.
Se
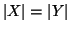 ,
allora esiste
,
allora esiste
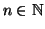 tale che X è equipotente a
In e Y è equipotente a In, ma allora X e Y sono tra loro
equipotenti (proposizione 2.3. Viceversa se sono equipotenti il
corollario precedente mostra che hanno la stessa cardinalità.
tale che X è equipotente a
In e Y è equipotente a In, ma allora X e Y sono tra loro
equipotenti (proposizione 2.3. Viceversa se sono equipotenti il
corollario precedente mostra che hanno la stessa cardinalità.

Sottinsiemi di un insieme finito
Proposizione 4.4
Sia
X un insieme finito e
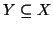
allora anche
Y è finito e
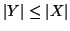
.
Se
Y è un sottoinsieme proprio di
X allora
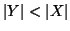
.
Dimostrazione. Procediamo per induzione su
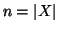 .
Se n=0 allora
.
Se n=0 allora
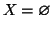 e
quindi anche
e
quindi anche
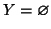 ,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
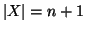 .
Sia
.
Sia
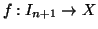 una bigezione e poniamo
xn=f(n) e
una bigezione e poniamo
xn=f(n) e
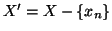 .
Chiaramente
.
Chiaramente
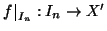 è una
bigezione, quindi
è una
bigezione, quindi
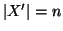 .
Si hanno due casi
.
Si hanno due casi
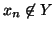 e
e 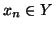 .
Nel primo caso
.
Nel primo caso
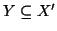 ,
quindi, per ipotesi
di induzione,
,
quindi, per ipotesi
di induzione,
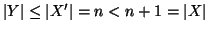 .
Nel secondo caso, detto
.
Nel secondo caso, detto
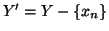 si ha che
si ha che
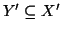 e quindi
e quindi
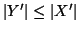 e
quindi
e
quindi
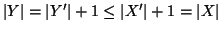 .
Si osservi che in
quest'ultimo caso, se
.
Si osservi che in
quest'ultimo caso, se 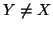 allora anche
allora anche 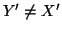 e quindi, per ipotesi di
induzione si ha che
e quindi, per ipotesi di
induzione si ha che
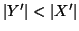 da cui
da cui
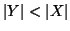 .
.

Come conseguenza si ha il seguente
Corollario 4.5
Un insieme finito non è equipotente ad alcun suo sottinsieme proprio.
Esempio 4.6
L'insieme
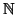
è infinito, si consideri ad esempio
l'applicazione
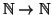
definita da
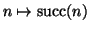
,
questa è una
bigezione tra
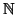
ed il sottinsieme proprio
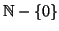
.
Esercizio 4.1
Si determinino altri sottinsiemi propri di
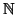
equipotenti a
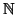 Soluzione
Soluzione
Esercizio 4.2
Siano
X e
Y insiemi finiti. Si provi che
- 1.
- se
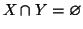 allora
allora
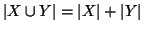 .
.
- 2.
- in generale
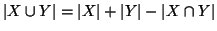
Soluzione
Esercizio 4.3
Siano
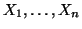
insiemi finiti a due a due disgiunti si provi che
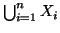
è finito e che
Soluzione
Esercizio 4.4
Se
X e
Y sono insiemi finiti, si provi che
- 1.
-
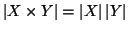 .
.
- 2.
-
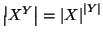
- 3.
-
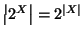 .
.
Soluzione
Esercizio 4.5
Siano
X e
Y insiemi finiti entrambi di cardinalità
n. Si provi che
ogni funzione iniettiva
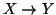
è anche surgettiva.
Soluzione
Esercizio 4.6
Sia
X un insieme finito di cardinalità
n. Si determini il numero delle
applicazioni biunivoche di
X in sé.
Soluzione



Next: Lezione 5 (12 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 3 (5 marzo
Domenico Luminati
2001-06-18
![]() ,
allora esiste
,
allora esiste
![]() tale che X è equipotente a
In e Y è equipotente a In, ma allora X e Y sono tra loro
equipotenti (proposizione 2.3. Viceversa se sono equipotenti il
corollario precedente mostra che hanno la stessa cardinalità.
tale che X è equipotente a
In e Y è equipotente a In, ma allora X e Y sono tra loro
equipotenti (proposizione 2.3. Viceversa se sono equipotenti il
corollario precedente mostra che hanno la stessa cardinalità.
![]()
![]() .
Se n=0 allora
.
Se n=0 allora
![]() e
quindi anche
e
quindi anche
![]() ,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
,
da cui si conclude. Supponiamo la tesi vera per n e
sia dato X con
![]() .
Sia
.
Sia
![]() una bigezione e poniamo
xn=f(n) e
una bigezione e poniamo
xn=f(n) e
![]() .
Chiaramente
.
Chiaramente
![]() è una
bigezione, quindi
è una
bigezione, quindi
![]() .
Si hanno due casi
.
Si hanno due casi
![]() e
e ![]() .
Nel primo caso
.
Nel primo caso
![]() ,
quindi, per ipotesi
di induzione,
,
quindi, per ipotesi
di induzione,
![]() .
Nel secondo caso, detto
.
Nel secondo caso, detto
![]() si ha che
si ha che
![]() e quindi
e quindi
![]() e
quindi
e
quindi
![]() .
Si osservi che in
quest'ultimo caso, se
.
Si osservi che in
quest'ultimo caso, se ![]() allora anche
allora anche ![]() e quindi, per ipotesi di
induzione si ha che
e quindi, per ipotesi di
induzione si ha che
![]() da cui
da cui
![]() .
.
![]()