

Next: Lezione 22
Up: Matematica Discreta (II modulo)
Previous: Lezione 20
Subsections
Definizione 21.1
Sia
un grafo, un sottografo
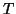
di
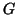
si dirà un
albero di
copertura di
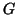
se
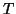 è un albero;
è un albero;
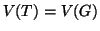 .
.
Osservazione 21.2
Chiaramente, se
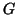
è un grafo che possiede un albero di copertura, allora
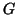
è connesso. Dato che due vertici di
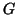
, essendo vertici di
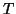
saranno
congiunti da un cammino in
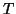
, e dato che
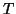
è un sottografo di
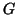
tale
cammino sarà un cammino anche in
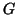
.
Esercizio 21.1
Si dia una dimostrazione formale di
quanto appena osservato. E si provi che se
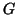
è un grafo e
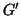
è un suo sottografo connesso tale che
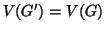
allora
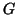
è connesso.
Soluzione
Teorema 21.3
Sia
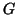
un grafo connesso finito allora
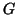
ha un albero di copertura.
Dimostrazione.
Diamo due dimostrazioni di questo teorema, entrambe costruttive: una che
costruisce un albero di copertura ``partendo dal basso'' ed una che lo
costruisce ``partendo dall'alto''.
Prima dimostrazione. Si consideri l'insieme
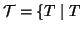
è sottografo di
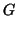
e
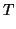
è un albero
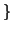
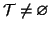 , infatti se
, infatti se
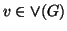 allora
allora
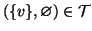 (i.e. è
un sottografo che è un albero). Dato che
(i.e. è
un sottografo che è un albero). Dato che 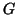 è finito, esiste
è finito, esiste
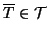 con
massimo numero di vertici, ossia tale che
Se proviamo che
con
massimo numero di vertici, ossia tale che
Se proviamo che
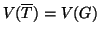 avremo trovato un albero di copertura.
Supponiamo che esista
avremo trovato un albero di copertura.
Supponiamo che esista
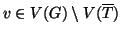 , allora, usando la
connessione di
, allora, usando la
connessione di 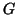 con la stessa tecnica usata nella dimostrazione del teorema
19.8, è possibile determinare un vertice
con la stessa tecnica usata nella dimostrazione del teorema
19.8, è possibile determinare un vertice
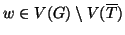 ed un vertice
ed un vertice 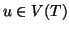 tali che
tali che
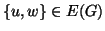 (si congiunge
(si congiunge
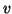 ad un vertice di
ad un vertice di
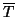 e si prendono il primo vertice del cammino che
arriva in
e si prendono il primo vertice del cammino che
arriva in
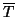 ed il suo predecessore). Ma allora
ed il suo predecessore). Ma allora
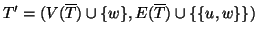 è evidentemente un sottografo di
è evidentemente un sottografo di 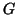 ed è un albero. Quest'ultimoa asserzione si prova esattamente come nella
seconda parte della dimostrazione del teorema di caratterizzazione
degli al;beri finiti). In altri termini
ed è un albero. Quest'ultimoa asserzione si prova esattamente come nella
seconda parte della dimostrazione del teorema di caratterizzazione
degli al;beri finiti). In altri termini
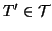 , d'altra
parte
, d'altra
parte
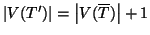 e questo
è in contraddizione con la massimalità di
e questo
è in contraddizione con la massimalità di
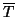 . Questo conclude la
prima dimostrazione.
. Questo conclude la
prima dimostrazione.
Seconda dimostrazione.
Si consideri l'insieme
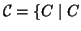
è sottografo connesso di
e
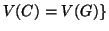
 dato che
dato che
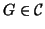 . Data la finitezza di
. Data la finitezza di 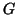 esisterà un grafo
esisterà un grafo
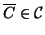 con il minor numero di lati, ovvero
Proviamo che
con il minor numero di lati, ovvero
Proviamo che
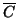 è un albero. Infatti se non lo fosse, per la
proprietà (3) del teorema di caratterizzazione degli alberi esisterebbe un
lato
è un albero. Infatti se non lo fosse, per la
proprietà (3) del teorema di caratterizzazione degli alberi esisterebbe un
lato
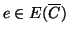 tale che
tale che
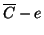 è connesso. Ma
è connesso. Ma
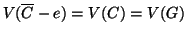 , quindi
, quindi
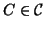 , e d'altra parte
, e d'altra parte
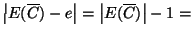 , che contraddice la minimalità di
, che contraddice la minimalità di
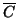 .
Questo conclude la seconda dimostrazione.
.
Questo conclude la seconda dimostrazione.

Osservazione 21.4
Il teorema precedente è vero anche senza l'ipotesi di finitezza, del grafo
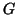
, la sua dimostrazione nel caso infinito, richiede però degli strumenti
un po' più sofisticati (si veda teorema
23.4).
Esercizio 21.2
Si traducano le due dimostrazioni del
teorema precedente in due algoritmi per la
determinazione di un albero di copertura di un grafo finito.
Soluzione
Esercizio 21.3
Si provi che se
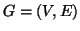
è un grafo connesso finito, allora
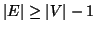
.
Soluzione
Alberi radicati
Definizione 21.5
Un
albero con radice è una coppia
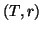
con
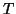
un albero e
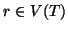
un vertice fissato che sarà detto
radice.
Se 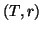 e
e 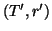 sono due alberi radicati, si dirà che sono isomorfi
(come alberi radicati) se esiste un isomorfismo di grafi
sono due alberi radicati, si dirà che sono isomorfi
(come alberi radicati) se esiste un isomorfismo di grafi 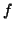 tra
tra 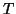 e
e 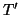 tale che
tale che 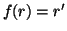 , e si scriverà
, e si scriverà
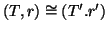 .
.
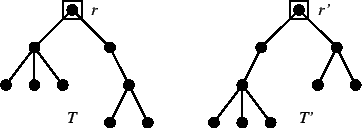
Esercizio 21.4
Si considerino i grafi in figura
12. Si provi che
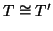
ma
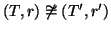
.
Figura 12:
Gli alberi radicati dell'esercizio 21.4
 |
Soluzione
La relazione 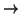 di ``paternità'' in un albero radicato
di ``paternità'' in un albero radicato
Dato un albero radicato, 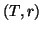 per ogni vertice
per ogni vertice 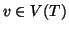 indichiamo con
indichiamo con
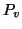 l'unico cammino che congiunge
l'unico cammino che congiunge 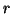 con
con 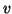 .
.
Dimostrazione.
Proviamo che ne vale almeno una. Se non vale la (1), allora
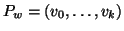 con
con 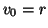 ,
, 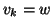 e
e 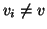 per ogni
per ogni 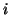 . Ma allora,
dato che
. Ma allora,
dato che
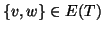 ,
,
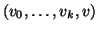 è un cammino che congiunge
è un cammino che congiunge 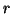 a
a 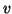 , per l'unicità di tale cammino
, per l'unicità di tale cammino
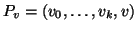 , e quindi vale la (2).
, e quindi vale la (2).
Proviamo ora che non possono valere contemporaneamente. Se vale la (1), allora
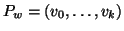 con
con 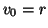 ,
, 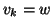 ed esiste un
ed esiste un 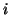 tale che
tale che 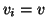 . Ma
allora
. Ma
allora
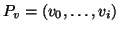 . Dato che,
. Dato che,
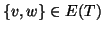 ,
, 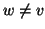 , quindi
, quindi
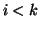 , e dato che
, e dato che 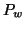 è un cammino
è un cammino
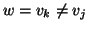 per ogni
per ogni 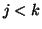 , quindi
, quindi 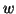 non compare in
non compare in
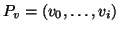 .
.

Definizione 21.7
Sia
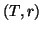
un albero radicato, e siano
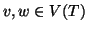
, diremo che
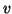
è
padre di
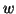
, o che
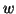
è figlio di
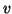
, e lo indicheremo con
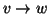
, se
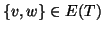
e
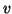
è un vertice di
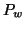
.
Proposizione 21.8
Sia
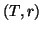
un albero radicato, e sia
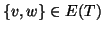
allora o
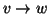
o
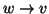
. Inoltre per ogni
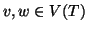
, se
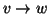
allora
.
Dimostrazione.
È semplicemente la proposizione precedente tradotta in termini della relazione
 .
.

Osservazione 21.9
La proposizione
21.8 può essere interpretata dicendo che ogni
albero radicato può essere dotato in modo naturale di una struttura di
grafo diretto, in modo che ad
ogni lato dell'albero corrisponda uno ed un solo lato del grafo diretto.

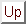

Next: Lezione 22
Up: Matematica Discreta (II modulo)
Previous: Lezione 20
Domenico Luminati
2004-03-18
![]() e
e ![]() sono due alberi radicati, si dirà che sono isomorfi
(come alberi radicati) se esiste un isomorfismo di grafi
sono due alberi radicati, si dirà che sono isomorfi
(come alberi radicati) se esiste un isomorfismo di grafi ![]() tra
tra ![]() e
e ![]() tale che
tale che ![]() , e si scriverà
, e si scriverà
![]() .
.![]() per ogni vertice
per ogni vertice ![]() indichiamo con
indichiamo con
![]() l'unico cammino che congiunge
l'unico cammino che congiunge ![]() con
con ![]() .
.
![]() con
con ![]() ,
, ![]() e
e ![]() per ogni
per ogni ![]() . Ma allora,
dato che
. Ma allora,
dato che
![]() ,
,
![]() è un cammino che congiunge
è un cammino che congiunge ![]() a
a ![]() , per l'unicità di tale cammino
, per l'unicità di tale cammino
![]() , e quindi vale la (2).
, e quindi vale la (2).
![]() con
con ![]() ,
, ![]() ed esiste un
ed esiste un ![]() tale che
tale che ![]() . Ma
allora
. Ma
allora
![]() . Dato che,
. Dato che,
![]() ,
, ![]() , quindi
, quindi
![]() , e dato che
, e dato che ![]() è un cammino
è un cammino
![]() per ogni
per ogni ![]() , quindi
, quindi ![]() non compare in
non compare in
![]() .
.
![]()
![]() .
.
![]()