

Next: Lezione 7
Up: Matematica Discreta (II modulo)
Previous: Lezione 5
Subsections
Insiemi numerabili
Definizione 6.1
Un insieme

si dice
numerabile se
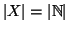
. La
cardinalità di
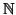
viene spesso indicata con
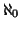
(si legge aleph
con zero). Quindi per dire che

è numerabile si scriverà anche
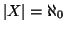
.
Il simbolo 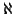 la prima lettera dell'alfabeto ebraico.
la prima lettera dell'alfabeto ebraico.
Diamo ora alcune proprietà degli insiemi numerabili.
Dimostrazione. Siano
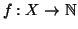 e
e
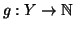 due bigezioni, allora si definisca
due bigezioni, allora si definisca
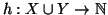 ponendo
ponendo
Si verifica facilmente che 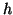 è una bigezione.
è una bigezione.

Proposizione 6.3
Se

e
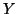
sono disgiunti,

numerabile e
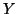
è finito, allora
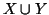
è numerabile.
Siano
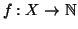 e
e
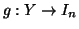 due bigezioni, allora si definisca
due bigezioni, allora si definisca
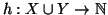 ponendo
Si verifica facilmente che
ponendo
Si verifica facilmente che 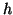 è una bigezione.
è una bigezione.

Dimostrazione.
Se 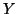 non è finito, allora contiene un sottinsieme numerabile
non è finito, allora contiene un sottinsieme numerabile 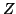 , ma allora
la tesi segue dal lemma 6.12.
, ma allora
la tesi segue dal lemma 6.12.

Proposizione 6.5
Se

è un insieme infinito ed
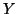
è un insieme finito o numerabile
allora
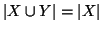
.
Dimostrazione. Possiamo supporre che 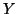 sia disgiunto da
sia disgiunto da  , in quanto
, in quanto
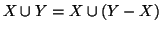 e per la proposizione precedente e la proposizione 4.4
e per la proposizione precedente e la proposizione 4.4
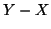 è finito o numerabile.
è finito o numerabile.
Sia
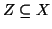 un sottinsieme numerabile, per le due proposizioni 6.3,
6.2, esiste una bigezione
un sottinsieme numerabile, per le due proposizioni 6.3,
6.2, esiste una bigezione
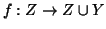 . Si definisca
allora
. Si definisca
allora
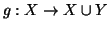 ponendo
ponendo
Proviamo che 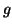 è iniettiva. Siano
è iniettiva. Siano
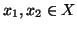 diversi, chiaramente,
dato che
diversi, chiaramente,
dato che  è iniettiva, se
è iniettiva, se
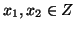 allora
allora
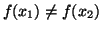 e quindi
e quindi
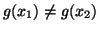 . Se
. Se
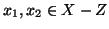 , evidentemente
, evidentemente
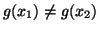 . Se
. Se
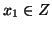 e
e
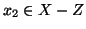 allora
allora
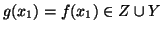 e, dato che
e, dato che 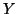 è
disgiunto da
è
disgiunto da  ,
,
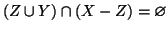 , e quindi
, e quindi
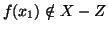 ,
mentre
,
mentre
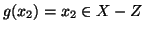 .
.
Proviamo che 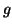 è surgettiva. Sia
è surgettiva. Sia
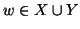 , allora si hanno due casi:
, allora si hanno due casi:
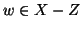 oppure
oppure
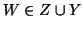 . Nel primo caso, preso
. Nel primo caso, preso 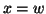 , si ha che
, si ha che
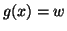 . Nel secondo caso, dato che
. Nel secondo caso, dato che  è surgettiva, esiste
è surgettiva, esiste 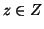 tale
che
tale
che 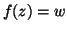 , e quindi
, e quindi 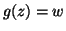 .
.

Proposizione 6.6
Se
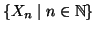
è una famiglia numerabile di insiemi finiti e a
due a due disgiunti, allora
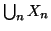
è numerabile.
Dimostrazione. Sia
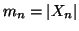 e per ogni
e per ogni 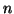 sia
sia
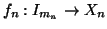 una
bigezione. Si considerino i numeri
una
bigezione. Si considerino i numeri
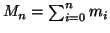 ,
, 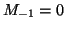 , e si
definisca
, e si
definisca
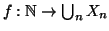 ponendo
ponendo
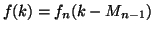
se
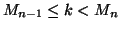
Una semplice verifica mostra che  è ben definita ed è una bigezione.
è ben definita ed è una bigezione.

Proposizione 6.7
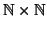
è numerabile, e quindi il prodotto di due insiemi numerabili
è numerabile.
Dimostrazione.
Per ogni
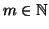 si consideri
si consideri
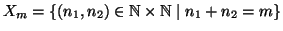 . Chiaramente
. Chiaramente
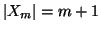 per ogni
per ogni 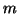 ,
,
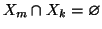 se
se
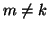 e infine
e infine
 (si osservi che
(si osservi che
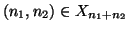 ). Ma allora la tesi segue dalla proposizione
precedente.
). Ma allora la tesi segue dalla proposizione
precedente.
Per quanto riguarda la seconda parte dell'enunciato, si osservi che se  e
e 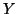 sono numerabili, e
sono numerabili, e
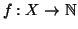 e
e
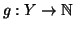 sono bigezioni, allora
l'applicazione prodotto
sono bigezioni, allora
l'applicazione prodotto
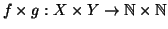 è
bigettiva.
è
bigettiva.

Proposizione 6.8
Se
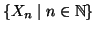
è una famiglia numerabile di insiemi numerabili e
a due a due disgiunti, allora
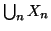
è numerabile.
Dimostrazione.
Per ogni
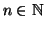 sia
sia
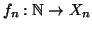 una bigezione, definiamo
una bigezione, definiamo
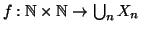 ponendo
ponendo
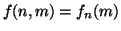 . Si conclude
verificando che
. Si conclude
verificando che  è una bigezione.
è una bigezione.

Esercizio 6.1
Si eseguano nel dettaglio tutte le verifiche necessarie a concludere le
dimostrazioni delle proposizioni di questa sezione.
Soluzione
Esercizio 6.2
Si provi che se
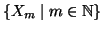
è una famiglia numerabile di insiemi
finiti, allora la loro unione è finita o numerabile.
Soluzione
Esercizio 6.3
Si provi che se
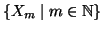
è una famiglia numerabile di insiemi
numerabili, allora la loro unione è numerabile.
Soluzione
Esercizio 6.4
Si provi che
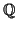
è numerabile.
Soluzione
Confronto di cardinalità: il Teorema di Cantor-Bernstein
Definizione 6.9
Dati due insiemi,

e
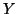
diremo che la cardinalità di

è
minore
o uguale alla cardinalità di
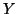
, e lo scriveremo
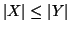
,
se esiste una funzione iniettiva,
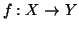
.
Diremo che la cardinalità di  è strettamente minore di quella di
è strettamente minore di quella di
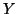 , e lo denoteremo con
, e lo denoteremo con
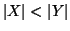 , se
, se
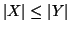 e
e
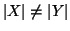 .
.
È immediato verificare che
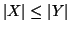 se e solo se
se e solo se 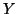 contiene un
sottinsieme equipotente a
contiene un
sottinsieme equipotente a  .
.
Esercizio 6.5
Si provi che nel caso di insiemi finiti, la nozione di ordinamento appena
introdotta tra le cardinalità, coincide con l'usuale ordinamento dei numeri
naturali.
Soluzione
Esercizio 6.6
Si provi che
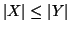
se e solo se esiste
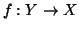
surgettiva.
Soluzione
Dimostrazione.
Basta osservare che l'identità è iniettiva e che composizione di funzioni
inettive è una funzione iniettiva.

Osservazione 6.11
La proposizione precedente mostra che la relazione di avere cardinalità
minore o uguale gode delle proprietà riflessiva e
transitiva. Vedremo tra poco che gode anche della proprietà
antisimmetrica.
Dimostrazione. Sia
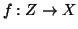 una bigezione. Poniamo
una bigezione. Poniamo
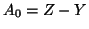 e
e
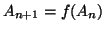 , e si ponga
, e si ponga
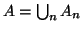 . Osserviamo che
. Osserviamo che
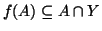 , e che
, e che  è una bigezione tra
è una bigezione tra 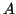 e la sua immagine. Definiamo
allora
e la sua immagine. Definiamo
allora 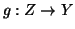 ponendo
ponendo
e proviamo che è una bigezione.
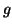 è iniettiva, siano infatti
è iniettiva, siano infatti
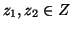 ,
,
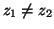 . Si hanno tre casi:
. Si hanno tre casi:
-
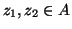 . In questo caso, dato che
. In questo caso, dato che  è iniettiva,
è iniettiva,
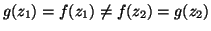 .
.
-
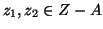 . In questo caso
. In questo caso
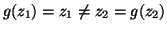 .
.
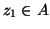 e
e
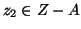 . In tal caso
. In tal caso
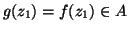 , mentre
, mentre
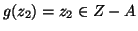 quindi
quindi
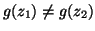 .
.
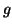 è surgettiva. Sia
è surgettiva. Sia  , allora o
, allora o 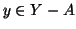 e allora
e allora
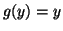 , oppure
, oppure 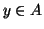 . In questo caso esiste
. In questo caso esiste
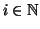 tale che
tale che 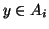 ,
inoltre dato che
,
inoltre dato che  e
e 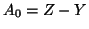 , sicuramente
, sicuramente  . Ma allora
. Ma allora
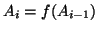 , quindi esiste
, quindi esiste
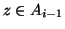 tale che
tale che 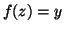 . Dato che
. Dato che
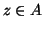 allora
allora
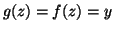 .
.

Teorema 6.13 (Cantor-Bernstein)
Siano

e
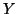
due insiemi e supponiamo che
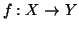
e
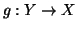
siano due
funzioni iniettive. Allora esiste una funzione bigettiva
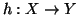
.
Dimostrazione.
Si osservi che
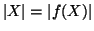 e che
e che
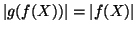 e
quindi
e
quindi
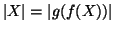 . D'altra parte,
. D'altra parte,
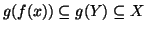 , quindi per il lemma precedente
, quindi per il lemma precedente
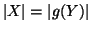 . Dato che
. Dato che
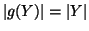 segue la tesi.
segue la tesi.

La tricotomia dei cardinali
Enunciamo senza dimostrare un importante teorema, la cuidimostrazione richiede
tecniche che esulano dalle finalità del corso, ma che è comunque importante
conoscere:
Teorema 6.14 (tricotomia dei cardinali)
Per ogni coppia di insiemi

,
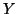
si ha che o
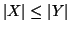
oppure
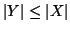
.
Osservazione 6.15
Come era naturale aspettarsi, la relazione di avere cardinalità minore
o uguale gode di tutte le proprietà di un ordinamento totale.
Il procedimento diagonale di Cantor
Le cardinalità finite e numerabile non esauriscono tutte le possibili
cardinalità, il seguente teorema dimostra che esistonoo insiemi di
cardinalità arbitrariamente elevata.
Dimostrazione.
La funzione
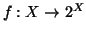 definita da
definita da
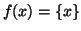 è iniettiva. Se
è iniettiva. Se
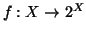 è una qualsiasi funzione allora non è surgettiva, infatti l'insieme
è una qualsiasi funzione allora non è surgettiva, infatti l'insieme
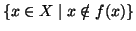 non appartiene all'immagine di
non appartiene all'immagine di  .
.

Osservazione 6.17
La tecnica di dimostrazione usata in questo teorema è nota come procedimento
diagonale. Il perché di tale nome appare chiaro se consideriamo la
dimostrazione nel caso particolare di
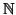
. Supponiamo di avere una
numerazione di sottinsiemi di
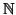
, rappresentiamo ogni sottinsieme di
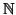
con una successione di 0 e
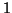 (mettiamo un
(mettiamo un 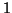 in corrispondenza
degli elementi che appartengono al sottinsieme e uno 0
altrimenti)
in corrispondenza
degli elementi che appartengono al sottinsieme e uno 0
altrimenti)
Costruiamo una nuova successione di 0 e
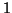
ponendo all'
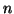
-esimo posto uno
0 se all'
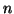
-esimo posto di
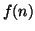
c'è un
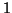
, e
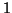
altrimenti. Chiaramente
tale successione è diversa da ciascuna delle
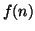
. La successione così costruita rappresenta proprio l'insieme
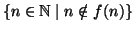
.
Esempio 6.18
La stessa tecnica diagonale può essere usata per provare che l'insieme dei
numeri reali è più che numerabile. Si supponga di avere un'applicazione
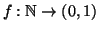
, e per ogni
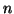
sia
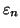
la
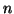
-esima cifra dello
sviluppo decimale infinito di
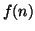
. Si ponga
Si costruisca quindi il numero reale
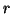
che ha
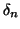
come
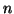
-esima
cifra del suo sviluppo decimale.
Chiaramente, questo numero sta nell'intervallo
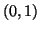
ma è diverso da tutti
gli
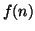
. in quanto differisce da
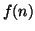
nella
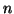
-esima cifra decimale. Per
concludere, si
osserva che
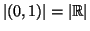
. Si può in realtà
dimostrare che
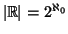
.
Esercizio 6.7
Si provi che
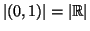
.
La funzione
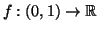
definita da
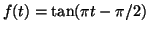
è una bigezione.

SoluzioneARRAY(0x8eaf5f0)
Esercizio 6.8
Siano
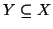
. Si provi che se
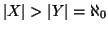
allora
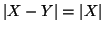
.
Soluzione
Esercizio 6.9
Siano
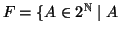
è finito
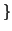
. Si provi che
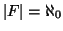 Soluzione
Soluzione
Esercizio 6.10
Si identifichi ogni numero reale in
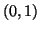
con la successione di
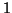
e 0 data del suo sviluppo binario, scegliendo quello infinito nei casi
di ambiguità (i.e.
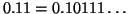
) e si usino i due esercizi
precedenti per provare che
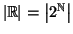
.
Soluzione


Next: Lezione 7
Up: Matematica Discreta (II modulo)
Previous: Lezione 5
Domenico Luminati
2004-03-18
![]() e
e
![]() due bigezioni, allora si definisca
due bigezioni, allora si definisca
![]() ponendo
ponendo
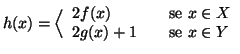
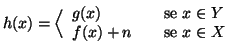
![]() non è finito, allora contiene un sottinsieme numerabile
non è finito, allora contiene un sottinsieme numerabile ![]() , ma allora
la tesi segue dal lemma 6.12.
, ma allora
la tesi segue dal lemma 6.12.
![]()
![]() sia disgiunto da
sia disgiunto da ![]() , in quanto
, in quanto
![]() e per la proposizione precedente e la proposizione 4.4
e per la proposizione precedente e la proposizione 4.4
![]() è finito o numerabile.
è finito o numerabile.
![]() un sottinsieme numerabile, per le due proposizioni 6.3,
6.2, esiste una bigezione
un sottinsieme numerabile, per le due proposizioni 6.3,
6.2, esiste una bigezione
![]() . Si definisca
allora
. Si definisca
allora
![]() ponendo
ponendo

![]() è surgettiva. Sia
è surgettiva. Sia
![]() , allora si hanno due casi:
, allora si hanno due casi:
![]() oppure
oppure
![]() . Nel primo caso, preso
. Nel primo caso, preso ![]() , si ha che
, si ha che
![]() . Nel secondo caso, dato che
. Nel secondo caso, dato che ![]() è surgettiva, esiste
è surgettiva, esiste ![]() tale
che
tale
che ![]() , e quindi
, e quindi ![]() .
.
![]()
![]() e per ogni
e per ogni ![]() sia
sia
![]() una
bigezione. Si considerino i numeri
una
bigezione. Si considerino i numeri
![]() ,
, ![]() , e si
definisca
, e si
definisca
![]() ponendo
ponendo
![]() si consideri
si consideri
![]() . Chiaramente
. Chiaramente
![]() per ogni
per ogni ![]() ,
,
![]() se
se
![]() e infine
e infine
![]() (si osservi che
(si osservi che
![]() ). Ma allora la tesi segue dalla proposizione
precedente.
). Ma allora la tesi segue dalla proposizione
precedente.
![]() e
e ![]() sono numerabili, e
sono numerabili, e
![]() e
e
![]() sono bigezioni, allora
l'applicazione prodotto
sono bigezioni, allora
l'applicazione prodotto
![]() è
bigettiva.
è
bigettiva.
![]()
![]() sia
sia
![]() una bigezione, definiamo
una bigezione, definiamo
![]() ponendo
ponendo
![]() . Si conclude
verificando che
. Si conclude
verificando che ![]() è una bigezione.
è una bigezione.
![]()
![]() è strettamente minore di quella di
è strettamente minore di quella di
![]() , e lo denoteremo con
, e lo denoteremo con
![]() , se
, se
![]() e
e
![]() .
.![]() se e solo se
se e solo se ![]() contiene un
sottinsieme equipotente a
contiene un
sottinsieme equipotente a ![]() .
.
![]()
![]() una bigezione. Poniamo
una bigezione. Poniamo
![]() e
e
![]() , e si ponga
, e si ponga
![]() . Osserviamo che
. Osserviamo che
![]() , e che
, e che ![]() è una bigezione tra
è una bigezione tra ![]() e la sua immagine. Definiamo
allora
e la sua immagine. Definiamo
allora ![]() ponendo
ponendo
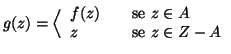
![]() è iniettiva, siano infatti
è iniettiva, siano infatti
![]() ,
,
![]() . Si hanno tre casi:
. Si hanno tre casi:
![]() è surgettiva. Sia
è surgettiva. Sia ![]() , allora o
, allora o ![]() e allora
e allora
![]() , oppure
, oppure ![]() . In questo caso esiste
. In questo caso esiste
![]() tale che
tale che ![]() ,
inoltre dato che
,
inoltre dato che ![]() e
e ![]() , sicuramente
, sicuramente ![]() . Ma allora
. Ma allora
![]() , quindi esiste
, quindi esiste
![]() tale che
tale che ![]() . Dato che
. Dato che
![]() allora
allora
![]() .
.
![]()
![]() e che
e che
![]() e
quindi
e
quindi
![]() . D'altra parte,
. D'altra parte,
![]() , quindi per il lemma precedente
, quindi per il lemma precedente
![]() . Dato che
. Dato che
![]() segue la tesi.
segue la tesi.
![]()
![]() definita da
definita da
![]() è iniettiva. Se
è iniettiva. Se
![]() è una qualsiasi funzione allora non è surgettiva, infatti l'insieme
è una qualsiasi funzione allora non è surgettiva, infatti l'insieme
![]() non appartiene all'immagine di
non appartiene all'immagine di ![]() .
.
![]()
![$\displaystyle \begin{array}{cccccccccc}
& & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \dots \...
...
\vdots & \ddots [10pt]
A & = & 0 & 1 & 1 & 0 & 0 & 1 & 1 & \dots
\end{array}$](img568.gif)
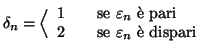
![$\displaystyle \begin{array}{ccccccccccc}
f(0) & = & 0. & \fbox 1 & 4 & 9 & 2 & ...
...ts & \ddots [10pt]
r & = & 0. & 2 & 2 & 1 & 1 & 1 & 2 & 1 & \dots
\end{array}$](img576.gif)