Lezione 13 (31 marzo 1999 h. 9.30-11.30)

   
Prime proprietà dei morfismi

Proposizione 13.1   Sia $\varphi:G\to G'$ un morfismo, allora:

1.

  $\varphi(1_G)=1_{G'}$

2.

  $\forall g\in G$ si ha $\varphi(g^{-1})=(\varphi(g))^{-1}$.

Dim.  1_G=1_G1_G e quindi $\varphi(1_G)=\varphi(1_G1_G)=\varphi(1_G)\varphi(1_G)$. Moltiplicando a sinistra per l'inverso di $\varphi(1_G)$ segue che $\varphi(1_G)=1_{G'}$.

1_G=gg^-1 e quindi $1_{G'}=\varphi(1_G)=\varphi(gg^{-1})=\varphi(g)\varphi(g^{-1}$. Moltiplicando entrambi i membri a sinistra per $(\varphi(g))^{-1}$ si ottiene $(\varphi(g))^{-1}=\varphi(g^{-1})$.     $\square$

Esempio 13.2   Proseguiamo l'esempio 12.6. Le conclusioni della proposizione precedente sono in questo caso le ben note relazioni:

$$\begin{eqnarray*}\exp(0) & = & e^0=1\\ \exp(-x) & = & e^{-x}=\frac{1}{e^x}=\frac{1}{\exp(x)} \end{eqnarray*}$$

   
Isomorfismi

Definizione 13.3   Un morfismo di gruppi si dice un isomorfismo se è bigettivo.

Proposizione 13.4   Se $\varphi:G\to G'$ è un isomorfismo, allora anche $\varphi^{-1}$ è un morfismo.

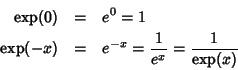
Dim.  Siano $g_1',g_2'\in G'$, e chiamiamo $g_1=\varphi^{-1}(g_1')$ e $g_2=\varphi^{-1}(g_2')$. Dato che $\varphi$ è un morfismo

$$\varphi(g_1g_2)=\varphi(g_1)\varphi(g_2)=g_1' g_2'$$

da cui, per l'invertibilità di $\varphi$ si ha $g_1g_2=\varphi^{-1}(g_1'g_2')$, che è la tesi.     $\square$

Esempio 13.5   Il morfismo $\exp$ dell'esempio 12.6 è invertibile, quindi è un isomorfismo. La sua inversa è l'applicazione logaritmo $\log :\mathbb R_+\to\mathbb R$, che, in accordo con la proposizione precedente, risulta essere anch'essa un morfismo:

$$\log(xy)=\log(x)+\log(y)$$

   
Nucleo di un morfismo

Definizione 13.6   Sia $\varphi:G\to G'$ un morfismo, si chiama nucleo di $\varphi$ l'insieme

$$\ker\varphi=\{g\in G\mid \varphi(g)=1\}.$$

Proposizione 13.7   Se $\varphi$ è un morfismo allora $\ker\varphi$ è un sottogruppo normale.

Dim.  La 1 della proposizione 13.1, garantisce che $i\in\ker\varphi$, e quindi $\ker\varphi\ne\varnothing$.

Siano $k_1,k_2\in\ker(\varphi)$, allora, usando la 2 di proposizione 13.1 ed il fatto che $\varphi(k_1)=\varphi(k_2)=1$,

$$\varphi(k_1k_2^{-1})=\varphi(k_1)\varphi(k_2^{-1})=\varphi(k_1)(\varphi(k_2))^{-1}=11^{-1}=1$$

ossia $k_1k_2^{-1}\in\ker(\varphi)$. Per il criterio del sottogruppo si ha che $\ker\varphi$ è un sottogruppo.

Sia ora $k\in \ker(\varphi)$ e $g\in G$, allora $\varphi(g^{-1}kg)=\varphi(g)^{-1}\varphi(k)\varphi(g)=1$, e quindi, per la proposizione 12.1, $\ker(\varphi)$ è normale.     $\square$

Proposizione 13.8   Un morfismo $\varphi$ è iniettivo se e solo se $\ker\varphi=\left\langle {}1\right\rangle$.

Dim.  Se $\varphi$ è iniettivo, allora necessariamente $\ker(\varphi)$ ha un solo elemento (si troverebbero altrimenti due elementi distinti aventi per immagine 1) e poiché $1\in\ker(\varphi)$ si ha che $\ker(\varphi)=\left\langle {}1\right\rangle$.

Viceversa siano $g_1,g_2\in G$ tali che $\varphi(g_1)=\varphi(g_2)$, allora

$$\varphi(g_2^{-1}g_1)=\varphi(g_2)^{-1}\varphi(g_1)=\varphi(g_1)^{-1}\varphi(g_1)=1$$

quindi $g_2^{-1}g_1\in\ker(\varphi)=\left\langle {}1\right\rangle$ e quindi g₂^-1g₁=1 da cui g₁=g₂.     $\square$

Osservazione 13.9   Nella dimostrazione precedente si è provato che se $\varphi(g_1)=\varphi(g_2)$ allora $g_2^{-1}g_1\in\ker(\varphi)$. Evidentemente vale anche il viceversa, in quanto se $g_2^{-1}g_1\in\ker(\varphi)$ allora

$$1=\varphi(g_2^{-1}g_1)=\varphi(g_2)^{-1}\varphi(g_1)$$

da cui $\varphi(g_1)=\varphi(g_2)$. In altre parole la relazione d'equivalenza $\stackrel{\varphi}{\sim}$, indotta da $\varphi$, coincide con la relazione d'equivalenza $\stackrel{K}{\sim}$, indotta dal sottogruppo $K=\ker(\varphi)$. Quindi gli insiemi $G\big/\mathchoice {{}_{\!\displaystyle {}\stackrel{\varphi}{\sim}}} {{}_{\!\t... ...ackrel{\varphi}{\sim}}} {{}_{\!\scriptscriptstyle {}\stackrel{\varphi}{\sim}}}$ e $G\big/\mathchoice {{}_{\!\displaystyle {}K}} {{}_{\!\textstyle {}K}} {{}_{\!\scriptstyle {}K}} {{}_{\!\scriptscriptstyle {}K}}$ coincidono.

   
Primo teorema di omomorfismo

Teorema 13.10 (primo teorema di omomorfismo)   Sia $\varphi:G\to G'$ un morfismo. Allora esiste un unico morfismo di gruppi $\widetilde{\varphi}:G\big/\mathchoice {{}_{\!\displaystyle {}\ker\varphi}} {{... ...\!\scriptstyle {}\ker\varphi}} {{}_{\!\scriptscriptstyle {}\ker\varphi}}\to G'$ tale che $\varphi=\widetilde{\varphi}\circ\pi$.

$$\begin{picture} (103,55)(-18,-6) \put(0,40){\makebox(0,0){$G... ...0){\vector(1,0){60}} \put(10,5){\vector(2,1){60}} \end{picture}$$ (17)

Si ha inoltre che:

1.

$\widetilde{\varphi{}}$ è iniettiva;

2.

$\widetilde{\varphi{}}$ è surgettiva se e solo se $\varphi$ è surgettiva.

Dim.  Per quanto osservato precedentemente, l'esistenza di una unica applicazione che faccia commutare il diagramma, e che tale applicazione verifichi le condizioni 1 e 2, è garantita dal teorema di omomorfismo per insiemi. Per avere la tesi, dobbiamo soltanto mostrare che tale applicazione è un morfismo, ossia che $\widetilde{\varphi{}}(g_1Hg_2H)=\widetilde{\varphi{}}(g_1H)\widetilde{\varphi{}}(g_2H)$. Ma, usando la commutatività del diagramma, ed il fatto osservato precedentemente, che $\pi$ è un morfismo, si ha:

$$\begin{eqnarray*}\widetilde{\varphi{}}(g_1Hg_2H) & = & \widetilde{\varphi{}}(\pi... ...i(g_2))= \widetilde{\varphi{}}(g_1H)\widetilde{\varphi{}}(g_2H) \end{eqnarray*}$$

che è la tesi.     $\square$

Osservazione 13.11   Si osservi che, dato che $\widetilde{\varphi{}}$ è sempre iniettiva, allora se $\varphi$ è surgettiva, la $\widetilde{\varphi{}}$ risulta essere bigettiva e quindi un isomorfismo.

   
Classificazione dei gruppi ciclici

Definizione 13.12   Un gruppo G è detto ciclico se esiste $g\in G$ tale che $G=\left\langle {}g\right\rangle$. Un tale elemento g viene chiamato un generatore di G.

Esempio 13.13   $\mathbb Z$ è un gruppo ciclico. Per ogni $n\in\mathbb N$, $n\ge 1$, il gruppo $\mathbb Z\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb Z}} {{}_{\!\textsty... ...} {{}_{\!\scriptstyle {}n\mathbb Z}} {{}_{\!\scriptscriptstyle {}n\mathbb Z}}$ è ciclico e $o(\mathbb Z\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb Z}} {{}_{\!\texts... ...{{}_{\!\scriptstyle {}n\mathbb Z}} {{}_{\!\scriptscriptstyle {}n\mathbb Z}})=n$.

Esercizio 13.1    Si provi che se $G=\left\langle {}g\right\rangle$ allora $G=\{g^n\mid n\in\mathbb Z\}$.
Soluzione

Proposizione 13.14   Sia G un gruppo ciclico, allora

$$G\oldcong\big\langle \begin{array}{ll} \mathbb Z\quad&\hbox{\... ...le {}n\mathbb Z}}\qquad&\hbox{\rm {se }} o(G)=n\ge1 \end{array}$$

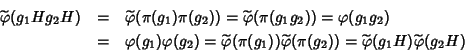
Dim.  Sia g un generatore di G, e si consideri l'applicazione $\varphi:\mathbb Z\to G$definita da $\varphi(h)=g^h$. Il fatto che g⁽h+k)=g^hg^k, per ogni $h,k\in\mathbb Z$ mostra che $\varphi$ è un morfismo. D'altra parte, dato che g è un generatore di G, $\varphi$ è surgettivo, ma allora per quanto osservato sopra, G è isomorfo a $\mathbb Z\big/\mathchoice {{}_{\!\displaystyle {}\ker\varphi}} {{}_{\!\textst... ... {{}_{\!\scriptstyle {}\ker\varphi}} {{}_{\!\scriptscriptstyle {}\ker\varphi}}$. D'altra parte i sottogruppi di $\mathbb Z$ sono tutti e soli della forma $n\mathbb Z$ con $n\ge 0$, quindi G è isomorfo o a $\mathbb Z\oldcong\mathbb Z\big/\mathchoice {{}_{\!\displaystyle {}0\mathbb Z}}... ...} {{}_{\!\scriptstyle {}0\mathbb Z}} {{}_{\!\scriptscriptstyle {}0\mathbb Z}}$, e ciò si ha solo se Gè infinito, oppure $G\oldcong\mathbb Z\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb Z}} {{}_{\... ...} {{}_{\!\scriptstyle {}n\mathbb Z}} {{}_{\!\scriptscriptstyle {}n\mathbb Z}}$ ed in tal caso o(G)=n.     $\square$

Osservazione 13.15   La proposizione precedente mostra che, a meno di isomorfismo, quelli dati nell'esempio sono tutti e soli i gruppi ciclici.

Esercizio 13.2    Si dimostri che se $\varphi:G\to G'$ è un morfismo di gruppi, allora se $H'\le G'$ allora $\varphi^{-1}(H')\le G$. Se H' è normale, allora anche $\varphi^{-1}(H')$ è normale.
Soluzione

Esercizio 13.3    Si dimostri che se $\varphi:G\to G'$ è un morfismo di gruppi e $H\le G$ allora $\varphi(H)\le G'$. È vero che se H è normale allora anche $\varphi(H)$ è normale?
Soluzione