


Next: Lezione 15 (14 aprile
Up: Matematica Discreta
Previous: Lezione 13 (31 marzo
Subsections
Definizione di anello
Definizione 14.1
Si chiama
anello una terna
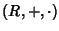
dove
R è un insieme e +,
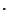
sono due operazioni su
R tali che:
- 1.
- (G,+) è un gruppo commutativo
- 2.
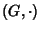 è un semigruppo
è un semigruppo
- 3.
- per ogni
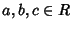 si ha
a(b+c)=ab + ac e
(b+c)a=ba+ca.
si ha
a(b+c)=ab + ac e
(b+c)a=ba+ca.
Le due proprietà del punto
3 si dicono
proprietà
distributive a sinistra e a destra. L'elemento neutro della somma sarà
denotato con 0 e l'inverso di
a per la somma sarà denotato con
-
a. Per brevità si scriverà
a-
b invece di
a+(-
b).
Un anello si dice
commutativo se l'operazione
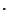
è commutativa.
Si dice che
R è un
anello con identità se esiste un elemento non
nullo che sia neutro per
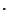
(i.e.
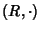
è un monoide). Tale
elemento neutro, che è
unico è
detto l'
identità dell'anello e denotato con 1.
Esercizio 14.1
Gli insiemi
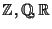
dotati delle usuali operazioni di somma e prodotto
sono tutti anelli commutativi con identità.
Le classi di resto modulo
n con le operazioni di somma e prodotto definite
nell'osservazione
6.9 è un anello commutativo con identità.
Il prodotto cartesiano
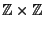
con le operazioni
(
a1,
a2)+(
b1,
b2)=(
a1+
b1,
a2+
b2) e
(
a1,
a2)(
b1,
b2)=(
a1b1,
a2b2) è un anello commutativo con
identità.
L'insieme delle matrici
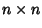
a coefficienti reali è un anello, in
generale non commutativo (è commutativo se e solo se
n=1.
Soluzione
Esercizio 14.2
Sia
R un anello e
X un insieme, si provi che
RX con le operazioni
definite da
è un anello. Se
R è commutativo, anche
RX lo è, se
R ha
un'identità, anche
RX ne ha una.
Soluzione
Proposizione 14.2
Sia
R un anello, allora
- 1.
- per ogni
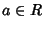 si ha a0=0a=0.
si ha a0=0a=0.
- 2.
- per ogni
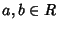 si ha
a(-b)=(-a)b=-(ab)
si ha
a(-b)=(-a)b=-(ab)
Dim.
Sia 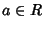 ,
allora a0=a(0+0), usando la proprietà
distributiva si ha allora
a(0+0)=a0+a0 e quindi,
a)=a0+a0. Dato che R è un gruppo rispetto alla somma, vale la
legge di cancellazione e quindi 0=a0. In modo del tutto analogo si prova che 0a=0.
,
allora a0=a(0+0), usando la proprietà
distributiva si ha allora
a(0+0)=a0+a0 e quindi,
a)=a0+a0. Dato che R è un gruppo rispetto alla somma, vale la
legge di cancellazione e quindi 0=a0. In modo del tutto analogo si prova che 0a=0.
Siano 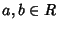 ,
allora usando quanto appena dimostrato e la
proprietà distributiva si ha che
0=a0=a(b+(-b))=ab+a(-b), da cui
-(ab)=a(-b). Analogamente si prova che
(-a)b=-(ab).
,
allora usando quanto appena dimostrato e la
proprietà distributiva si ha che
0=a0=a(b+(-b))=ab+a(-b), da cui
-(ab)=a(-b). Analogamente si prova che
(-a)b=-(ab).

Definizione 14.3
Sia
R un anello, un sottinsieme
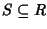
sarà detto un
sottoanello se è contemporaneamente un sottogruppo di (
R,+) e un
sottosemigruppo di
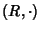
.
Se
R è un anello con identità, si
richiede anche che
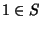
.
In altre parole:
- 1.
-
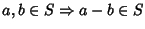
- 2.
-
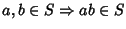
- 3.
-
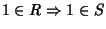 .
.
Definizione 14.4
Un elemento
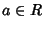
è detto un
divisore di 0 se
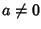
ed
esiste
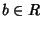
,
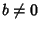
tale che
ab=0 oppure
ba=0.
Un anello commutativo con identità che non contiene divisori di zero viene
detto un
dominio di integrità.
Definizione 14.5
Sia
R un anello con identità. Un elemento
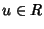
sarà detto una
unità se è
invertibile
rispetto al prodotto, ossia se esiste
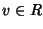
tale che
uv=
vu=1. Tale
elemento
v se esiste
è unico e viene denotato con
u-1.
Esempio 14.6
La matrice
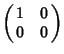
è un divisore di 0 nell'anello delle
matrici
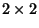
.
Infatti
Tutte le coppie del tipo (a,0) sono dei divisori di 0 nell'anello
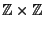 ,
infatti
(a,0)(0,b)=(0,0) per ogni
,
infatti
(a,0)(0,b)=(0,0) per ogni
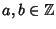 ,
quindi
,
quindi
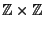 non è un dominio di integrità.
non è un dominio di integrità.
Le unità di 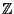 sono soltanto 1,-1. Le unità di
sono soltanto 1,-1. Le unità di
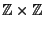 sono
(1,1), (1,-1), (-1,-1) e (-1,1).
sono
(1,1), (1,-1), (-1,-1) e (-1,1).
Esercizio 14.3
Si provi che
![$\left[a\right]\in\mathbb Z\big/\mathchoice
{{}_{\!\displaystyle {}n\mathbb Z}}...
...}
{{}_{\!\scriptstyle {}n\mathbb Z}}
{{}_{\!\scriptscriptstyle {}n\mathbb Z}}$](img572.gif)
è una unità se e solo se il
massimo comun divisore (
a,
n)=1.
Soluzione
Esercizio 14.4
Si provi che
![$\left[a\right]\in\mathbb Z\big/\mathchoice
{{}_{\!\displaystyle {}n\mathbb Z}}...
...yle {}n\mathbb Z}}
{{}_{\!\scriptscriptstyle {}n\mathbb Z}}-\{\left[0\right]\}$](img573.gif)
è un
divisore di 0 se e solo se
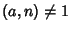
.
Soluzione
Proposizione 14.7
L'insieme degli elementi invertibili di un anello con identità
R, è un
gruppo con l'operazione prodotto. Tale gruppo viene denotato con
R* ed
è chiamato il
gruppo delle unità di
R.
Dim.
Indichiamo con
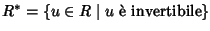 .
Se
.
Se
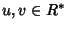 allora esistono u-1 e
allora esistono u-1 e
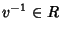 tali che
uu-1=u-1u=vv-1=v-1v=1, ma allora
(uv)(v-1u-1)=u(vv-1)u-1=u1u-1=uu-1=1 e analogamente anche
(v-1u-1)(uv)=1, quindi uv è una unità ovvero
tali che
uu-1=u-1u=vv-1=v-1v=1, ma allora
(uv)(v-1u-1)=u(vv-1)u-1=u1u-1=uu-1=1 e analogamente anche
(v-1u-1)(uv)=1, quindi uv è una unità ovvero 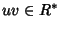 .
.
Evidentemente 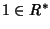 e se u è una unità anche u-1 lo è,
quindi la tesi.
e se u è una unità anche u-1 lo è,
quindi la tesi.

Esercizio 14.5
Si confronti la dimostrazione della proposizione precedente con la soluzione
dell'esercizio
8.4 e si spieghi perché sono ``così simili''.
Soluzione
Osservazione 14.8
Lo 0 non è mai invertibile, dato che
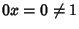
per ogni
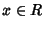
.
Definizione 14.9
Un anello con identità viene detto un
corpo se ogni suo elemento
diverso da 0 è invertibile. Un corpo viene detto un
campo se è
commutativo.
Lemma 14.10
Sia
R un anello con identità, e sia
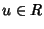
una
unità. Allora
u non è un divisore di 0.
Dim.
Sia u una unità e sia b tale che ub=0, allora
b=u-1ub=u-10=0,
e quindi u non è un divisore di 0.

Corollario 14.11
In un corpo non ci sono divisori di 0, e quindi ogni campo è un dominio
di integrità.
Dim.
Ogni elemento diverso da 0 di un corpo è invertibile, e,
per quanto appena visto, gli elementi
invertibili non sono divisori di zero.

Esercizio 14.6
Si provi che
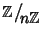
è un campo se e solo se
n è primo.
Soluzione
Esercizio 14.7
Si provi che il gruppo delle unità di
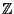
è isomorfo a
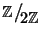
.
Soluzione



Next: Lezione 15 (14 aprile
Up: Matematica Discreta
Previous: Lezione 13 (31 marzo
Domenico Luminati
1999-07-08
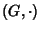 è un semigruppo
è un semigruppo
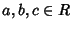 si ha
a(b+c)=ab + ac e
(b+c)a=ba+ca.
si ha
a(b+c)=ab + ac e
(b+c)a=ba+ca.
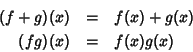
![]() ,
allora a0=a(0+0), usando la proprietà
distributiva si ha allora
a(0+0)=a0+a0 e quindi,
a)=a0+a0. Dato che R è un gruppo rispetto alla somma, vale la
legge di cancellazione e quindi 0=a0. In modo del tutto analogo si prova che 0a=0.
,
allora a0=a(0+0), usando la proprietà
distributiva si ha allora
a(0+0)=a0+a0 e quindi,
a)=a0+a0. Dato che R è un gruppo rispetto alla somma, vale la
legge di cancellazione e quindi 0=a0. In modo del tutto analogo si prova che 0a=0.
![]() ,
allora usando quanto appena dimostrato e la
proprietà distributiva si ha che
0=a0=a(b+(-b))=ab+a(-b), da cui
-(ab)=a(-b). Analogamente si prova che
(-a)b=-(ab).
,
allora usando quanto appena dimostrato e la
proprietà distributiva si ha che
0=a0=a(b+(-b))=ab+a(-b), da cui
-(ab)=a(-b). Analogamente si prova che
(-a)b=-(ab).
![]()
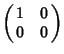 è un divisore di 0 nell'anello delle
matrici
è un divisore di 0 nell'anello delle
matrici ![]() ,
infatti
(a,0)(0,b)=(0,0) per ogni
,
infatti
(a,0)(0,b)=(0,0) per ogni
![]() ,
quindi
,
quindi
![]() non è un dominio di integrità.
non è un dominio di integrità.
![]() sono soltanto 1,-1. Le unità di
sono soltanto 1,-1. Le unità di
![]() sono
(1,1), (1,-1), (-1,-1) e (-1,1).
sono
(1,1), (1,-1), (-1,-1) e (-1,1).![]() .
Se
.
Se
![]() allora esistono u-1 e
allora esistono u-1 e
![]() tali che
uu-1=u-1u=vv-1=v-1v=1, ma allora
(uv)(v-1u-1)=u(vv-1)u-1=u1u-1=uu-1=1 e analogamente anche
(v-1u-1)(uv)=1, quindi uv è una unità ovvero
tali che
uu-1=u-1u=vv-1=v-1v=1, ma allora
(uv)(v-1u-1)=u(vv-1)u-1=u1u-1=uu-1=1 e analogamente anche
(v-1u-1)(uv)=1, quindi uv è una unità ovvero ![]() .
.
![]() e se u è una unità anche u-1 lo è,
quindi la tesi.
e se u è una unità anche u-1 lo è,
quindi la tesi.
![]()
![]()
![]()