


Next: Lezione 17 (21 aprile
Up: Matematica Discreta
Previous: Lezione 15 (14 aprile
Subsections
Sia R un anello commutativo con identità. Consideriamo l'insieme
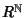 delle successioni a valori in R. Se
delle successioni a valori in R. Se
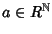 denoteremo con an il
valore della funzione a sul naturale n.
denoteremo con an il
valore della funzione a sul naturale n.
Sull'insieme
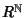 possiamo definire due operazioni:
possiamo definire due operazioni:
Per la commutatività della somma nell'anelle R il termine
n-esimo del prodotto di due serie formali si può anche scrivere:
intendendo in tal modo dire che la somma è estesa a tutte le coppie di
indici i,j la cui somma è n.
Proposizione 16.1
L'insieme
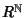
con le due operazioni appena definite è un anello
commutativo con identità. Tale anello viene chiamato l'anello delle
serie formali a coefficienti in
R.
Dim.
La verifica che la somma definisca una struttura di gruppo abeliano in cui lo 0 è la
successione costantemente nulla (i.e. 0n=0 per ogni n) ad in cui
l'opposto della successione a è la successione
(-a)n=-an è lasciata
per esercizio.
Dalla definizione e dal fatto che R è commutativo segue immediatamente che
il prodotto di serie formali è commutativo.
Proviamo che il prodotto è associativo.
quindi
(a(bc))n=((ab)c)n per ogni n e quindi
(a(bc))=((ab)c).
Proviamo ora la proprietà distributiva.
dato che questa relazione vale per ogni n allora
a(b+c)=ab+ac. L'altr
aproprietà distributiva segue dalla commutatività del prodotto.
Consideriamo la successione 1 definita da
allora
poiché tale relazione vale per ogni n allora 1a=a. Che anche a1=asegue dalla commutatività del prodotto.

Definizione 16.2
Chiameremo
polinomio una serie formale definitivamente nulla (i.e.
esiste
n tale che
ak=0 per ogni
k>
n). Se
a è un polinomio,
chiameremo
grado di
a il numero
con la convenzione che
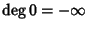
.
Proposizione 16.3
Se
a e
b sono polinomi, allora anche
a+
b e
ab lo sono e
Se
R è un dominio di integrità, allora nella (
23) vale
l'uguaglianza.
Dim.
Se
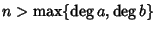 necessariamente an=0 e bn=0 e quindi an+bn=0 per ogni
necessariamente an=0 e bn=0 e quindi an+bn=0 per ogni
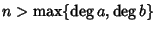 ,
quindi a+b è un polinomio e vale la
(22).
,
quindi a+b è un polinomio e vale la
(22).
Sia
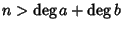 e consideriamo
e consideriamo
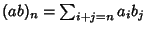 .
Se
.
Se
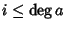 e
e
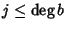 allora
allora
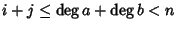 ,
quindi in ogni
addendo della somma che esprime (ab)n o
,
quindi in ogni
addendo della somma che esprime (ab)n o 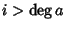 o
o 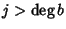 ossia
almeno uno tra ai e bj è nullo. Quindi tutti gli addendi sono nulli e
pertanto (ab)n=0. Pertanto ab è un polinomio e vale la (23).
ossia
almeno uno tra ai e bj è nullo. Quindi tutti gli addendi sono nulli e
pertanto (ab)n=0. Pertanto ab è un polinomio e vale la (23).
Sia R un dominio di integrità e siano 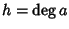 e
e 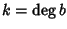 e
consideriamo
e
consideriamo
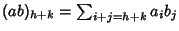 .
Di tutti gli addendi di questa
somma, l'unico che può essere non nullo è quello che si ottiene con i=he j=k (in tutti gli altri casi possibili si ha che o i>h e quindi ai=0o j>k e quindi bj=0). E quindi
.
Di tutti gli addendi di questa
somma, l'unico che può essere non nullo è quello che si ottiene con i=he j=k (in tutti gli altri casi possibili si ha che o i>h e quindi ai=0o j>k e quindi bj=0). E quindi
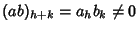 in quanto
in quanto 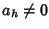 ,
,
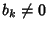 e R è un dominio di integrità.
e R è un dominio di integrità.

Proposizione 16.4
L'insieme dei polinomi è un
sottoanello dell'anello delle
serie formali.
Dim.
La proposizione precedente mostra che l'insieme dei polinomi
è chiuso per somma e prodotto. D'altra parte è evidente che le successioni
0 e 1 sono dei polinomi e che se a è un polinomio allora anche -a lo
è.

Osservazione 16.5
Indichiamo ora con
P l'anello dei polinomi a coefficienti in
R, e
consideriamo l'applicazione
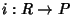
definita da
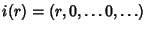
,
ossia
i(
r) è la successione tale che
i(
r)
0=
r e
i(
r)
n=0 per ogni
n>0.
L'applicazione
i è un morfismo di anelli. Infatti
e quindi
i(
r1=
r2)=
i(
r1)=
i(
r2).
Chiaramente il morfismo
i è iniettivo, quindi è un isomorfismo con la
sua immagine, possiamo, e d'ora in poi lo faremo, identificare
R con la sua
immagine
i(
R). Osserviamo ancora che se
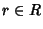
e
a è un polinomio,
allora
Dim.
Procediamo per induzione su i. Per i=0, dalla definizione di
potenza)e:expg, segue che x0=1.
Supponiamo latesi vera per i allora
ma per ipotesi di induzione
quindi in definitiva

Osservazione 16.7
L'
osservazione e la
proposizione precedenti
permettono allora di scrivere ogni polinomio nel modo usuale. Infatti
D'ora in poi si userà questa notazione per i polinomi, e si indicherà con
R[
x] l'anello dei polinomi a coefficienti in
R.
L'anello delle serie formali si denota invece con R[[x]]. Il nome serie
formali deriva dal fatto che una serie può essere pensata come una ``somma
infinita'' del tipo
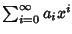 essenso x come nella
proposizione precedente. È chiaro che questa è però soltanto una comoda
notazione, in quanto in un anello non si possono fare somme infinite.
essenso x come nella
proposizione precedente. È chiaro che questa è però soltanto una comoda
notazione, in quanto in un anello non si possono fare somme infinite.
Osservazione 16.8
Dalla (
16.3) segue che se
R è un dominio di integrità allora
anche
R[
x] lo è. Infatti se
![$P,Q\in R[x]$](img682.gif)
e sono non nulli, allora
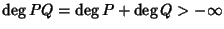
e quindi
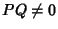
.
D'altra parte è chiaro che se
R non è un dominio allora a maggior
ragione non lo è
R[
x] che contiene
R come sottanello.



Next: Lezione 17 (21 aprile
Up: Matematica Discreta
Previous: Lezione 15 (14 aprile
Domenico Luminati
1999-07-08
![]() possiamo definire due operazioni:
possiamo definire due operazioni:
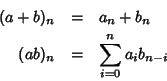
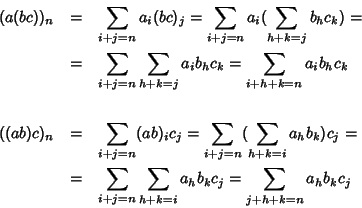
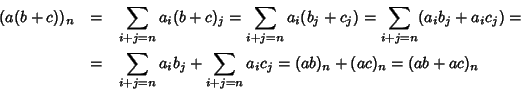
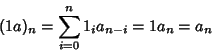
![]() necessariamente an=0 e bn=0 e quindi an+bn=0 per ogni
necessariamente an=0 e bn=0 e quindi an+bn=0 per ogni
![]() ,
quindi a+b è un polinomio e vale la
(22).
,
quindi a+b è un polinomio e vale la
(22).
![]() e consideriamo
e consideriamo
![]() .
Se
.
Se
![]() e
e
![]() allora
allora
![]() ,
quindi in ogni
addendo della somma che esprime (ab)n o
,
quindi in ogni
addendo della somma che esprime (ab)n o ![]() o
o ![]() ossia
almeno uno tra ai e bj è nullo. Quindi tutti gli addendi sono nulli e
pertanto (ab)n=0. Pertanto ab è un polinomio e vale la (23).
ossia
almeno uno tra ai e bj è nullo. Quindi tutti gli addendi sono nulli e
pertanto (ab)n=0. Pertanto ab è un polinomio e vale la (23).
![]() e
e ![]() e
consideriamo
e
consideriamo
![]() .
Di tutti gli addendi di questa
somma, l'unico che può essere non nullo è quello che si ottiene con i=he j=k (in tutti gli altri casi possibili si ha che o i>h e quindi ai=0o j>k e quindi bj=0). E quindi
.
Di tutti gli addendi di questa
somma, l'unico che può essere non nullo è quello che si ottiene con i=he j=k (in tutti gli altri casi possibili si ha che o i>h e quindi ai=0o j>k e quindi bj=0). E quindi
![]() in quanto
in quanto ![]() ,
,
![]() e R è un dominio di integrità.
e R è un dominio di integrità.
![]()
![]()
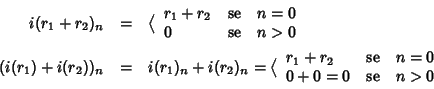
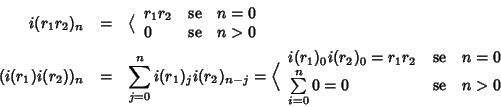
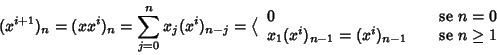
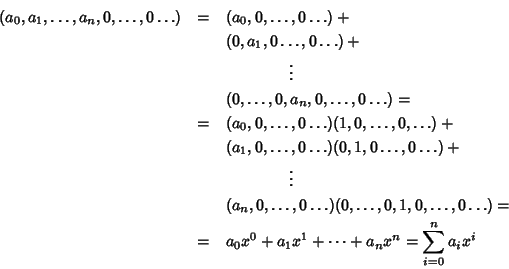
![]() essenso x come nella
proposizione precedente. È chiaro che questa è però soltanto una comoda
notazione, in quanto in un anello non si possono fare somme infinite.
essenso x come nella
proposizione precedente. È chiaro che questa è però soltanto una comoda
notazione, in quanto in un anello non si possono fare somme infinite.