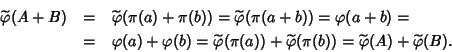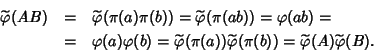Next: Lezione 16 (19 aprile
Up: Matematica Discreta
Previous: Lezione 14 (12 aprile
Subsections
Definizione 15.1
Siano
R,
R' anelli, una applicazione
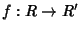
sarà detta un
morfismo
di anelli se:
- 1.
-
f(a+b)=f(a)+f(b) (ossia
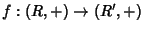 è un morfismo di gruppi).
è un morfismo di gruppi).
- 2.
-
f(ab)=f(a)f(b) (ossia
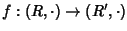 è un morfismo di
semigruppi).
è un morfismo di
semigruppi).
Se
R ed
R' sono anelli con identità, diremo che
f è un
morfismo
di anelli con identità se in più:
- 1.
- f(1)=1, (ossia
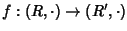 è un morfismo di monoidi).
è un morfismo di monoidi).
Sia
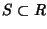 un sottogruppo rispetto alla somma. Dato che la somma è
commutativa, S è un sottogruppo normale, quindi è definito il gruppo quoziente
un sottogruppo rispetto alla somma. Dato che la somma è
commutativa, S è un sottogruppo normale, quindi è definito il gruppo quoziente
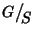 in modo che la proiezione a quoziente
in modo che la proiezione a quoziente
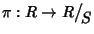 sia un morfismo di gruppi. E precisamente ponendo
sia un morfismo di gruppi. E precisamente ponendo
|
(a+S)+(b+S)=(a+b)+S.
|
(18) |
Si vuole definire anche un'altra operazione su
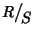 in modo che
con tali operazioni risulti un anello e che la proiezione sia un morfismo di
anelli. Ossia si vuole che la seguente
in modo che
con tali operazioni risulti un anello e che la proiezione sia un morfismo di
anelli. Ossia si vuole che la seguente
sia una buona definizione.
Osservazione 15.2
Osserviamo che, come nel caso dei gruppi, tale
formula definisce effettivamente una operazione se e solo se
ossia se e solo se
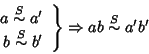 |
(20) |
Teorema 15.4
La (
19) è una buona definizione se e solo se
S è un ideale.
Dim.
Supponiamo che S sia un ideale e proviamo che allora vale la
(20). Infatti se
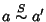 e
e
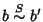 allora
allora 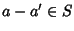 e
e 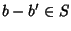 e quindi esistono
e quindi esistono 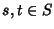 tali che
a-a'=s e b-b'=t, ovvero a=a'+s e b=b'+s. Ma allora, usando le
proprietà distributive sia a sinistra che a destra, si ha:
tali che
a-a'=s e b-b'=t, ovvero a=a'+s e b=b'+s. Ma allora, usando le
proprietà distributive sia a sinistra che a destra, si ha:
ab=(a'+s)(b'+t)=a'b'+a't+sb'+st
de cui
dato che S è un sottogruppo rispetto alla somma e, per la proprietà
(2) della definizione di ideale,
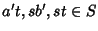 .
Quindi
.
Quindi
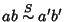 .
.
Viceversa, supponiamo che la (19) sia una buona definizione, ossia
che valga la (20). Allora se 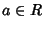 e
e 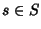 si ha che
si ha che
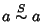 e
e
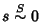 ,
quindi
,
quindi
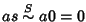 ossia
ossia 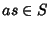 .
Analogamente si prova che anche
.
Analogamente si prova che anche
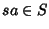 .
.

Teorema 15.5
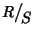
con le operazioni definita da (
18) e
(
19) è un anello e la proiezione a quoziente è un morfismo di
anelli.
Dim.
Che
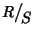 sia un gruppo commutativo rispetto alla somma, segue dai
risultati che si hanno per i quozienti di gruppi.
sia un gruppo commutativo rispetto alla somma, segue dai
risultati che si hanno per i quozienti di gruppi.
Proviamo che il prodotto è associativo. Siano
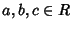 ,
allora
,
allora
Proviamo ora che vale la proprietà distributiva.Siano
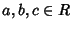 ,
allora
,
allora
Che la proiezione a quoziente sia un morfismo segue immediatamente dalla definizione.

Definizione 15.6
Sia
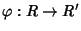
un morfismo di anelli. Si chiama
nucleo di
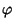
l'insieme
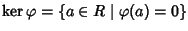
.
Proposizione 15.7
Il nucleo di un morfismo è un ideale.
Dim.
Se
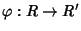 è un morfismo di anelli, allora in particolare è un
morfismo di gruppi, rispetto alla somma, quindi
è un morfismo di anelli, allora in particolare è un
morfismo di gruppi, rispetto alla somma, quindi
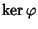 è un sottogruppo
di R rispetto alla somma (si veda l'analogo risultato per i
gruppi).
è un sottogruppo
di R rispetto alla somma (si veda l'analogo risultato per i
gruppi).
Siano ora 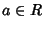 e
e
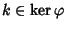 ,
allora
,
allora
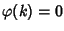 e quindi
e quindi
ossia
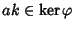 .
Allo stesso modo si prova che anche
.
Allo stesso modo si prova che anche
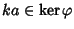 e
quindi che
e
quindi che
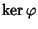 è un ideale.
è un ideale.

Osservazione 15.9
Quanto visto sopra, ci dice anche che il morfismo
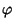
è iniettivo se e
solo se
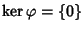
.
Teorema 15.10 (primo teorema di omomorfismo)
Sia
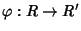
un morfismo di anelli. Allora esiste un unico morfismo di
anelli
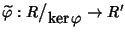
tale che
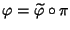
.
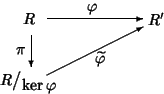 |
(21) |
Si ha inoltre che:
- 1.
-
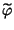 è iniettiva;
è iniettiva;
- 2.
-
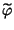 è surgettiva se e solo se
è surgettiva se e solo se 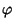 è surgettiva.
è surgettiva.
Dim.
La dimostrazione è sostanzialmente identica a quella dell'analogo
teorema per i gruppi, in
ogni caso la ripetiamo.
L'esistenza di una
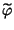 che faccia commutare il diagramma e che
verifichi le condizioni (1) e (2), segue dal teorema di omomorfismo
per insiemi e
dall'osservazione 15.8. Verifichiamo che
che faccia commutare il diagramma e che
verifichi le condizioni (1) e (2), segue dal teorema di omomorfismo
per insiemi e
dall'osservazione 15.8. Verifichiamo che
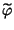 è un
morfismo di anelli. Siano
è un
morfismo di anelli. Siano
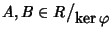 ,
e siano
,
e siano 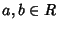 tali che
tali che 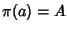 e
e 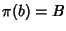 ,
allora, utilizzando il fatto che
,
allora, utilizzando il fatto che 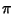 e
e
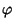 sono dei morfismi e la commutatività del diagramma (21), si
ha:
sono dei morfismi e la commutatività del diagramma (21), si
ha:
Analogamente
Ciò conclude la dimostrazione.

Esercizio 15.1
Si provi che se
I è un ideale di
R allora
- 1.
- se R è commutativo allora
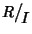 è commutativo.
è commutativo.
- 2.
- se R è con identità, allora anche
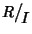 è con
identità e la proiezione a quoziente è un morfismo di anelli con
identità.
è con
identità e la proiezione a quoziente è un morfismo di anelli con
identità.
Soluzione
Esercizio 15.2
Sia
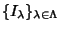
una famiglia di ideali dell'anello
R. Si provi che
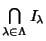
è un
ideale di
R.
Soluzione
Esercizio 15.3
Sia
R un anello e
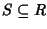
un suo sottinsieme. Si definisca (
S) l'ideale generato da
S e, si usi l'esercizio precedente per provarne
l'esistenza.
Soluzione
Esercizio 15.4
Sia
R un anello commutativo, si provi che
dove
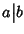
sta a significare che esiste
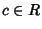
tale che
b=
ca. (Si confronti con la definizione
3.1).
Soluzione
Esercizio 15.5
Siano
I,
J ideali dell'anello commutativo
R. Si definiscano
Si provi che
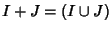
,
ossia è l'ideale generato da
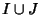
.
Soluzione
Esercizio 15.6
Sia
R un anello con identità. Si provi che se
I è un ideale di
R che contiene una unità, allora
I =
R.
Soluzione
Esercizio 15.7
Si usi l'esercizio precedente per provare che
R è un corpo se e solo se
gli unici ideali che possiede sono (0) e
R.
Soluzione



Next: Lezione 16 (19 aprile
Up: Matematica Discreta
Previous: Lezione 14 (12 aprile
Domenico Luminati
1999-07-08
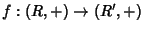 è un morfismo di gruppi).
è un morfismo di gruppi).
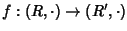 è un morfismo di
semigruppi).
è un morfismo di
semigruppi).
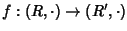 è un morfismo di monoidi).
è un morfismo di monoidi).
![]() un sottogruppo rispetto alla somma. Dato che la somma è
commutativa, S è un sottogruppo normale, quindi è definito il gruppo quoziente
un sottogruppo rispetto alla somma. Dato che la somma è
commutativa, S è un sottogruppo normale, quindi è definito il gruppo quoziente
![]() in modo che la proiezione a quoziente
in modo che la proiezione a quoziente
![]() sia un morfismo di gruppi. E precisamente ponendo
sia un morfismo di gruppi. E precisamente ponendo
![]() e
e
![]() allora
allora ![]() e
e ![]() e quindi esistono
e quindi esistono ![]() tali che
a-a'=s e b-b'=t, ovvero a=a'+s e b=b'+s. Ma allora, usando le
proprietà distributive sia a sinistra che a destra, si ha:
tali che
a-a'=s e b-b'=t, ovvero a=a'+s e b=b'+s. Ma allora, usando le
proprietà distributive sia a sinistra che a destra, si ha:
![]() e
e ![]() si ha che
si ha che
![]() e
e
![]() ,
quindi
,
quindi
![]() ossia
ossia ![]() .
Analogamente si prova che anche
.
Analogamente si prova che anche
![]() .
.
![]()
![]() sia un gruppo commutativo rispetto alla somma, segue dai
risultati che si hanno per i quozienti di gruppi.
sia un gruppo commutativo rispetto alla somma, segue dai
risultati che si hanno per i quozienti di gruppi.
![]() ,
allora
,
allora
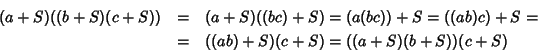
![]() ,
allora
,
allora
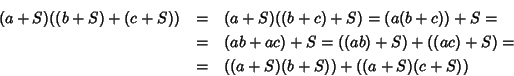
![]() è un morfismo di anelli, allora in particolare è un
morfismo di gruppi, rispetto alla somma, quindi
è un morfismo di anelli, allora in particolare è un
morfismo di gruppi, rispetto alla somma, quindi
![]() è un sottogruppo
di R rispetto alla somma (si veda l'analogo risultato per i
gruppi).
è un sottogruppo
di R rispetto alla somma (si veda l'analogo risultato per i
gruppi).
![]() e
e
![]() ,
allora
,
allora
![]() e quindi
e quindi
![]() che faccia commutare il diagramma e che
verifichi le condizioni (1) e (2), segue dal teorema di omomorfismo
per insiemi e
dall'osservazione 15.8. Verifichiamo che
che faccia commutare il diagramma e che
verifichi le condizioni (1) e (2), segue dal teorema di omomorfismo
per insiemi e
dall'osservazione 15.8. Verifichiamo che
![]() è un
morfismo di anelli. Siano
è un
morfismo di anelli. Siano
![]() ,
e siano
,
e siano ![]() tali che
tali che ![]() e
e ![]() ,
allora, utilizzando il fatto che
,
allora, utilizzando il fatto che ![]() e
e
![]() sono dei morfismi e la commutatività del diagramma (21), si
ha:
sono dei morfismi e la commutatività del diagramma (21), si
ha: