


Next: Lezione 18 (22 aprile
Up: Matematica Discreta
Previous: Lezione 16 (19 aprile
Subsections
Teorema 17.1
Siano
R e
R' due anelli commutativi con identità, e sia
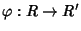
un morfismo di anelli con identità. Allora per ogni
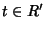
esiste un
unico morfismo
![$\varphi_t:R[x]\to R'$](img686.gif)
tale che
- 1.
-
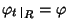
- 2.
-
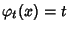
Dim.
Definiamo
![$\varphi_t:R[x]\to R'$](img686.gif) ponendo
ponendo
l'applicazione è ben definita in quanto, trattandosi di polinomi, la somma a
secondo membro è finita. Evidentemente l'applicazione 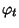 così
definita verifica le proprietè (1) e (2). Proviamo che
così
definita verifica le proprietè (1) e (2). Proviamo che 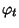 è un
morfismo.
è un
morfismo.
Siano
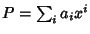 e
e
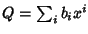
D'altra parte
dove la terzultima uguaglianza è ootenuta perché l'anello R' è
commutativo e l'ultima uguaglanza è ottenuta semplicemente riordinando i
termini della somma (cosa che si può fare perché la somma è
commutativa). Evidentemente si ha allora che
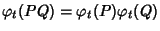 .
.
Proviamo ora l'unicità. Sia
![$\psi:R[x]\to R'$](img697.gif) un morfismo con le proprietà
richieste. Osserviamo che se
un morfismo con le proprietà
richieste. Osserviamo che se
 ,
dato che
,
dato che 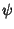 è un
morfismo deve risultare:
è un
morfismo deve risultare:
ossia
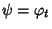 .
.

Osservazione 17.2
Un caso particolare del precedente teorema è quando
R=
R' e
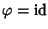
.
In tal caso se
![$P\in R[x]$](img703.gif)
il valore di
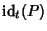
viene solitamente
indicato con
P(
t) e viene chiamato la
valutazione in
t di
P (e
il morfismo
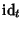
viene chiamato il morfismo di valutazione in
t).
P(
t) è ciò che si ottiene dando alla ``variabile''
x il valore
t.
Si osservi che in questo modo ad ogni polinomio
![$P\in R[x]$](img703.gif)
si associa una
funzione
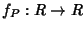
definita da
fP(
t)=
P(
t). Si definisce così una
applicazione
![$R[x]\to R^R$](img707.gif)
che al polinomio
P associa la funzione
polinomiale
fP. Osserviamo che tale applicazione non è in generale
iniettiva, ossia si possono avere polinomi diversi che definiscono la stessa
funzione. Ad esempio si considerino i due polinomi
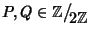
dati da
P=0 e
Q=
x2+
x. Chiaramente
P(0)=
P(1)=0 ma anche
Q(0)=0 e
Q(1)=1
2+1=1+1=0, pur tuttavia i due
polinomi sono diversi.
Esercizio 17.1
Si provi che l'applicazione
![$f:R[x]\to R^R$](img709.gif)
definita nell'osservazione
precedente (
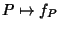
essendo
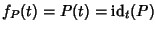
)
è un morfismo di
anelli.
Soluzione
Teorema 17.3 (divisione euclidea)
Sia
K un campo e siano
![$P_1,P_2\in K[x]$](img712.gif)
con
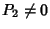
,
allora esistono
unici
![$Q,R\in K[x]$](img714.gif)
tali che
P1 = P2 Q + R
con
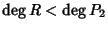
.
Dim.
Esistenza. Osserviamo innanzitutto che se
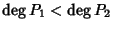 la tesi segue
prendendo Q = 0 e R = P1. Supponiamo allora che
la tesi segue
prendendo Q = 0 e R = P1. Supponiamo allora che
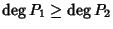 e
procediamo per induzione su
e
procediamo per induzione su
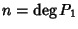 .
Se
.
Se
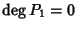 allora
allora
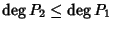 e quindi
e quindi
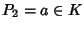 e dato che
e dato che 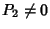 ,
,
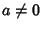 e quindi è
invertibile. Ma allora
e quindi è
invertibile. Ma allora
P1 = a (a-1 P1) + 0 = P2 (a-1 P1) + 0.
Sia ora
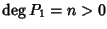 e supponiamo che la tesi sia vera per ogni
polinomio P con
e supponiamo che la tesi sia vera per ogni
polinomio P con
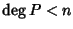 .
Siano allora
.
Siano allora
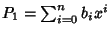 e
e
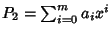 con
con 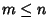 e
e 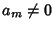 .
Dato che
.
Dato che 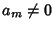 è
invertibile, si consideri allora il polinomio
P=P1 - bnam-1xn-m
P2. Si osservi che
è
invertibile, si consideri allora il polinomio
P=P1 - bnam-1xn-m
P2. Si osservi che
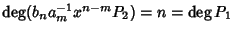 e quindi il polinomio P ha grado non
superiore a n. Ma d'altra parte
il termine di grado n è dato da
bnxn+(-bnam-1xn-mamxm)=0 e
quindi
e quindi il polinomio P ha grado non
superiore a n. Ma d'altra parte
il termine di grado n è dato da
bnxn+(-bnam-1xn-mamxm)=0 e
quindi
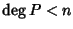 .
Possiamo quindi applicare l'ipotesi di induzione per dire
che allora esistono
.
Possiamo quindi applicare l'ipotesi di induzione per dire
che allora esistono
![$Q,R\in K[x]$](img714.gif) tali che P=QP2+R con
tali che P=QP2+R con
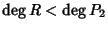 .
Ma allora
.
Ma allora
e quindi la tesi.
Unicità. Supponiamo che esistano
![$Q,R,Q',R'\in K[x]$](img729.gif) con
con
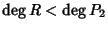 e
e
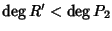 tali che
P1=P2Q+R=P2Q'+R'. Da quest'ultima relazione
segue immediatamente che
P2(Q - Q')=R' - R e quindi, passando ai gradi,
tali che
P1=P2Q+R=P2Q'+R'. Da quest'ultima relazione
segue immediatamente che
P2(Q - Q')=R' - R e quindi, passando ai gradi,
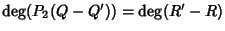 .
Ma ora, usando le relazioni sui
gradi,
.
Ma ora, usando le relazioni sui
gradi,
ma allora
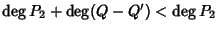 .
Dato che
.
Dato che 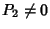 ciò
implica che
ciò
implica che
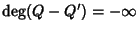 ossia Q=Q', da cui segue che allora
anche R=R'.
ossia Q=Q', da cui segue che allora
anche R=R'.

Definizione 17.4
Sia
![$P\in R[x]$](img703.gif)
un polinomio. Diremo che
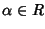
è una
radice
di
P se
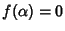
.
Si dirà anche che
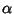
è uno
zero di
P.
Teorema 17.5 (di Ruffini)
Sia
K un campo e sia
![$P\in K[x]$](img738.gif)
allora
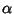
è una radice di
P se
e solo se
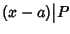
(i.e. esiste
Q tale che
P=(
x-
a)
Q, si veda
anche l'esercizio
15.4).
Dim.
Si esegua la divisione euclidea di P per
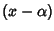 allora si ottiene
allora si ottiene
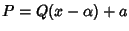 con
con 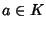 ,
dato che
,
dato che
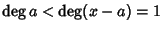 .
Si osservi
allora che
.
Si osservi
allora che
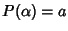 e quindi
e quindi
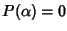 se e solo se a=0 ossia se e
solo se
se e solo se a=0 ossia se e
solo se
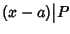 .
.




Next: Lezione 18 (22 aprile
Up: Matematica Discreta
Previous: Lezione 16 (19 aprile
Domenico Luminati
1999-07-08
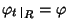
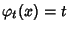
![]() ponendo
ponendo
![]() e
e
![]()
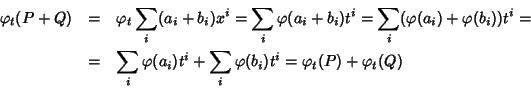
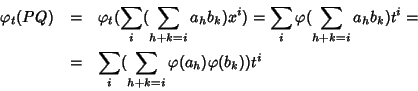
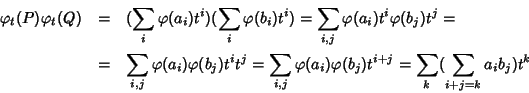
![]() un morfismo con le proprietà
richieste. Osserviamo che se
un morfismo con le proprietà
richieste. Osserviamo che se
![]() ,
dato che
,
dato che ![]() è un
morfismo deve risultare:
è un
morfismo deve risultare:
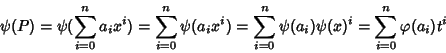
![]() la tesi segue
prendendo Q = 0 e R = P1. Supponiamo allora che
la tesi segue
prendendo Q = 0 e R = P1. Supponiamo allora che
![]() e
procediamo per induzione su
e
procediamo per induzione su
![]() .
Se
.
Se
![]() allora
allora
![]() e quindi
e quindi
![]() e dato che
e dato che ![]() ,
,
![]() e quindi è
invertibile. Ma allora
e quindi è
invertibile. Ma allora
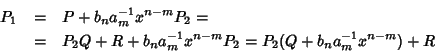
![]() con
con
![]() e
e
![]() tali che
P1=P2Q+R=P2Q'+R'. Da quest'ultima relazione
segue immediatamente che
P2(Q - Q')=R' - R e quindi, passando ai gradi,
tali che
P1=P2Q+R=P2Q'+R'. Da quest'ultima relazione
segue immediatamente che
P2(Q - Q')=R' - R e quindi, passando ai gradi,
![]() .
Ma ora, usando le relazioni sui
gradi,
.
Ma ora, usando le relazioni sui
gradi,
![\begin{displaymath}\begin{array}{l}
\deg P_2(Q - Q') = \deg P_2 + \deg (Q-Q') \...
...pt]
\deg(R'-R) \le \max\{\deg R,\deg R'\}<\deg P_2
\end{array}\end{displaymath}](img732.gif)
![]() allora si ottiene
allora si ottiene
![]() con
con ![]() ,
dato che
,
dato che
![]() .
Si osservi
allora che
.
Si osservi
allora che
![]() e quindi
e quindi
![]() se e solo se a=0 ossia se e
solo se
se e solo se a=0 ossia se e
solo se
![]() .
.
![]()