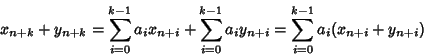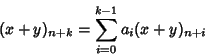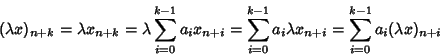Dim.
Supponiamo che ![]() abbia molteplicità
abbia molteplicità
![]() e proviamo che
allora è radice di tutte le derivate fino all'ordine m-1. Procediamo per
induzione su m. Se m=1 la tesi è data dal teorema di
Ruffini. Supponiamo la tesi vera per
m. Sia quindi
e proviamo che
allora è radice di tutte le derivate fino all'ordine m-1. Procediamo per
induzione su m. Se m=1 la tesi è data dal teorema di
Ruffini. Supponiamo la tesi vera per
m. Sia quindi
![]() ,
ovvero
,
ovvero
![]() allora
derivando si ottiene
allora
derivando si ottiene
Viceversa. Procediamo per induzione su m. Per m=1 la tesi è
ovvia. Supponiamo la tesi vera per ![]() .
Sia P un polinomio e sia
.
Sia P un polinomio e sia
![]() tale che
tale che
Sia
![]() una successione, diremo che x risolve una equazione
ricorsiva, se ogni elemento è funzione dei precedenti, in simboli se
esistono delle funzioni
una successione, diremo che x risolve una equazione
ricorsiva, se ogni elemento è funzione dei precedenti, in simboli se
esistono delle funzioni
![]() tali che
tali che
Supponendo di avere date le equazioni ricorsive, il problema di ricavare informazioni sulle successioni che le risolvono non è in generale di facile soluzione. Analizzeremo un caso di equazioni ricorsive di tipo particolare, per le quali si riescono a determinare esplicitamente tutte le soluzioni.
Considereremo equazioni ricorsive che hanno storia finita ovvero per le
quali esiste un ![]() tale che ogni termine è funzione soltanto dei kprecedenti (i.e. le fn hanno come dominio tutte
tale che ogni termine è funzione soltanto dei kprecedenti (i.e. le fn hanno come dominio tutte
![]() )
e in cui le fnsono tutte uguali e lineari, ossia equazioni del tipo
)
e in cui le fnsono tutte uguali e lineari, ossia equazioni del tipo
Anche se nella pratica le equazioni ricorsive che si incontrano sono definite
sui numeri reali (si pensi al calcolo della complessità di un algoritmo,
ossia il numero di passi necessario per ottenere l'output in funzione
dell'input), può essere comodo ambientare il problema nel campo dei numeri
complessi. Nel seguito denoteremo con ![]() un campo che può essere o quello
dei numeri reali o quello dei numeri complessi.
un campo che può essere o quello
dei numeri reali o quello dei numeri complessi.
Supponiamo allora di avere fissata l'equazione ricorsiva (27), ossia
di aver fissati
![]() e di cercare le successioni
e di cercare le successioni
![]() che verificano la (27). Sia
che verificano la (27). Sia
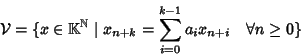
Dim.
Siano
![]() allora per ogni n si ha
allora per ogni n si ha
![]() e
e
![]() sommando membro a membro si
ha allora che
sommando membro a membro si
ha allora che