


Next: Lezione 19 (26 aprile
Up: Matematica Discreta
Previous: Lezione 17 (21 aprile
Subsections
Proposizione 18.1
Sia
K un campo e sia
![$P\in K[x]$](img738.gif)
un polinomio non nullo. Allora se
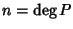
,
P ha al più
n radici.
Dim.
Procediamo per induzione su 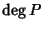 .
Se
.
Se 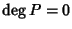 P non ha
radici. Supponiamo che
P non ha
radici. Supponiamo che
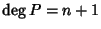 ,
se P non ha radici, allora la tesi è
vera. Supponiamo allora che
,
se P non ha radici, allora la tesi è
vera. Supponiamo allora che 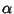 sia una radice di P; per il
teorema di Ruffini esiste un
polinomio Q tale che
sia una radice di P; per il
teorema di Ruffini esiste un
polinomio Q tale che
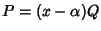 .
Dato che K è un campo, è in
particolare un dominio di integrità e quindi per le relazioni sui
gradi si ha che
.
Dato che K è un campo, è in
particolare un dominio di integrità e quindi per le relazioni sui
gradi si ha che 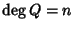 ,
quindi Q ha, per ipotesi di induzione, al più n radici. Osserviamo
ancora che se
,
quindi Q ha, per ipotesi di induzione, al più n radici. Osserviamo
ancora che se
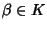 allora
allora
e sempre per il fatto che K è un dominio di integrità, si ha che
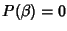 se e solo se
se e solo se
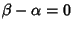 oppure
oppure
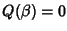 ossia se e solo
se
ossia se e solo
se
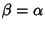 oppure
oppure 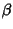 è una radice di Q. Quindi P ha al più
n+1 radici.
è una radice di Q. Quindi P ha al più
n+1 radici.

Osservazione 18.2
Segue immediatamente dalla proposizione precedente, che se
P è un
polinomio ha con
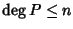
che ha
n+1 radici distinte, allora
P=0.
Corollario 18.3 (principio di identità dei polinomi)
Sia
K un campo con infiniti elementi. Se
![$P,Q\in K[x]$](img760.gif)
sono tali che
P(
t)=
Q(
t) per ogni
t allora
P=
Q
Dim.
Si applichi l'osservazione precedente al polinomio P-Q, per il quale si
possono trovare infinite radici.

Osservazione 18.4
Il corollario precedente mostra che se
K è infinito, allora
l'applicazione dell'osservazione
17.2 è iniettiva.
Esercizio 18.1
Si provi che il morfismo
![$K[x]\to K^K$](img761.gif)
definito nell'osservazione
17.2
e nell'esercizio
17.1, è iniettivo se e solo se il campo
K è
infinito. Quando il campo
K è finito si determini il nucleo di tale
morfismo.
Soluzione
Lemma 18.5
Sia
K un campo e siano
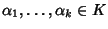
.
Si consideri la
matrice
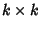
a coefficienti in
K
La matrice
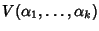
è invertibile se e solo se gli
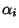
sono tra loro distinti.
Dim.
Consideriamo il sistema lineare
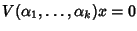 e supponiamo
che
e supponiamo
che
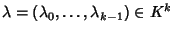 sia una sua soluzione,
ciò vuol dire che
sia una sua soluzione,
ciò vuol dire che
Si consideri il polinomio
![$P(x)=\sum_{i=0}^{k-1}\lambda_i x^i\in K[x]$](img770.gif) ,
allora il sistema precedente non dice altro che ogni
,
allora il sistema precedente non dice altro che ogni 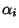 è una radice
di P. Dato che
è una radice
di P. Dato che
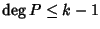 ,
se gli
,
se gli 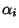 sono distinti, per
l'osservazione 18.2, P=0 ossia
sono distinti, per
l'osservazione 18.2, P=0 ossia
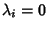 per ogni i. Quindi il
sistema lineare ha solo la soluzione banale e quindi la matrice è
invertibile.
per ogni i. Quindi il
sistema lineare ha solo la soluzione banale e quindi la matrice è
invertibile.
Viceversa, se due dedgli 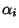 sono uguali, la matrice ha due righe
uguali e quindi non è invertibile.
sono uguali, la matrice ha due righe
uguali e quindi non è invertibile.

Definizione 18.6
Sia
![$P\in K[x]$](img738.gif)
un polinomio non nullo a coefficienti in un campo e sia
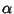
una sua radice. Si chiama
molteplicità della radice
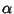
il massimo tra gli interi
m tali che
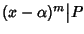
.
Definizione 18.7
Sia
![$P\in R[x]$](img703.gif)
,
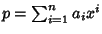
.
Definiamo
derivata formale del
polinomio
P il polinomio
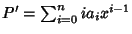
.
Proposizione 18.8
Si provi che se
![$P,Q\in R[x]$](img682.gif)
allora
Dim.
Lasciata per esercizio.

Proposizione 18.9
Sia
![$P\in K[x]$](img738.gif)
un polinomio a coefficienti in un campo, e sia
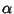
una
sua radice.
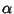
ha molteplicità maggiore di 1 se e solo se
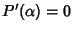
.
Dim.
Dato che 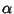 è una radice allora per il teorema di
Ruffini
è una radice allora per il teorema di
Ruffini
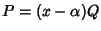 .
Derivando si
ha
.
Derivando si
ha
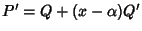 e quindi
e quindi
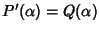 e per tanto
e per tanto 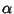 è radice di P' se e solo se è radice di Q e quindi, ancora per il
teorema di Ruffini, se e solo
se esiste R tale che
è radice di P' se e solo se è radice di Q e quindi, ancora per il
teorema di Ruffini, se e solo
se esiste R tale che
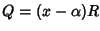 ovvero se e solo se
ovvero se e solo se
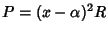 ,
che è la tesi.
,
che è la tesi.

Esercizio 18.2
Sia
K un campo e sia
![$Q\in K[x]$](img782.gif)
siano
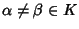
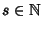
.
Detto
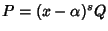
si provi che
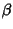
è radice di
P con
molteplicità
m se e solo se
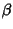
è radice di
Q con molteplicità
m.
Soluzione
Definizione 18.10
Sia
K un campo. Si consideri l'insieme
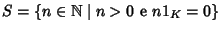
.
Se
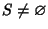
allora
ha minimo. Tale minimo si chiama
caratteristica di
K, e
si indica con
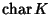
.
Se invece
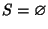
si dirà che
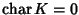
.
Esercizio 18.3
Si provi che la caratteristica di un campo è un numero primo.
Soluzione
Esercizio 18.4
Si provi che se
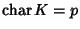
allora per ogni
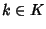
si ha che
pk=0.
Soluzione
Teorema 18.11
Sia
K un campo di caratteristica 0 e sia
![$P\in K[x]$](img738.gif)
e
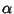
una sua
radice e indichiamo con
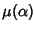
la sua molteplicità. Allora
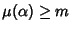
se e solo se
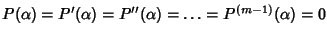
.



Next: Lezione 19 (26 aprile
Up: Matematica Discreta
Previous: Lezione 17 (21 aprile
Domenico Luminati
1999-07-08
![]() .
Se
.
Se ![]() P non ha
radici. Supponiamo che
P non ha
radici. Supponiamo che
![]() ,
se P non ha radici, allora la tesi è
vera. Supponiamo allora che
,
se P non ha radici, allora la tesi è
vera. Supponiamo allora che ![]() sia una radice di P; per il
teorema di Ruffini esiste un
polinomio Q tale che
sia una radice di P; per il
teorema di Ruffini esiste un
polinomio Q tale che
![]() .
Dato che K è un campo, è in
particolare un dominio di integrità e quindi per le relazioni sui
gradi si ha che
.
Dato che K è un campo, è in
particolare un dominio di integrità e quindi per le relazioni sui
gradi si ha che ![]() ,
quindi Q ha, per ipotesi di induzione, al più n radici. Osserviamo
ancora che se
,
quindi Q ha, per ipotesi di induzione, al più n radici. Osserviamo
ancora che se
![]() allora
allora
![]()

![]() e supponiamo
che
e supponiamo
che
![]() sia una sua soluzione,
ciò vuol dire che
sia una sua soluzione,
ciò vuol dire che
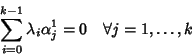
![]() sono uguali, la matrice ha due righe
uguali e quindi non è invertibile.
sono uguali, la matrice ha due righe
uguali e quindi non è invertibile.
![]()
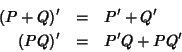
![]()
![]() è una radice allora per il teorema di
Ruffini
è una radice allora per il teorema di
Ruffini
![]() .
Derivando si
ha
.
Derivando si
ha
![]() e quindi
e quindi
![]() e per tanto
e per tanto ![]() è radice di P' se e solo se è radice di Q e quindi, ancora per il
teorema di Ruffini, se e solo
se esiste R tale che
è radice di P' se e solo se è radice di Q e quindi, ancora per il
teorema di Ruffini, se e solo
se esiste R tale che
![]() ovvero se e solo se
ovvero se e solo se
![]() ,
che è la tesi.
,
che è la tesi.
![]()