Dim.
Per definizione di
![]() ,
dati
,
dati ![]() e
e
![]() ,
si ha che
,
si ha che
![]() se e solo se
se e solo se ![]() .
Ma allora le due relazioni
date dal lemma precedente possono
essere riscritte
.
Ma allora le due relazioni
date dal lemma precedente possono
essere riscritte
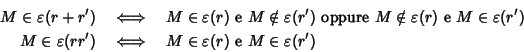
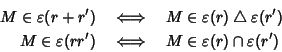
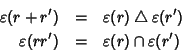
Proviamo ora che
![]() porta l'identità di R nell'identità di
porta l'identità di R nell'identità di
![]() ,
ossia che
,
ossia che
![]() .
Infatti se
.
Infatti se
![]() allora
allora
![]() quindi
quindi
![]() , ossia
, ossia
![]() .
.
![]() è iniettivo. Supponiamo che
è iniettivo. Supponiamo che
![]() ,
allora, dato che
,
allora, dato che
![]() è un morfismo di anelli con identità,
è un morfismo di anelli con identità,
![]() .
Allora 1+r è invertibile, altrimenti
esisterebbe un ideale massimale che lo contiene. Ma allora per
l'esercizio 22.3 1+r=1 e quindi r=0.
.
Allora 1+r è invertibile, altrimenti
esisterebbe un ideale massimale che lo contiene. Ma allora per
l'esercizio 22.3 1+r=1 e quindi r=0.
Proviamo l'ultima parte dell teorema. Dato che R è finito, anche
![]() lo è e quindi anche tutti i suoi sottoinsiemi lo sono. Sia allora
lo è e quindi anche tutti i suoi sottoinsiemi lo sono. Sia allora
![]() e proviamo per induzione sul numero di elementi di X che
allora esiste
e proviamo per induzione sul numero di elementi di X che
allora esiste ![]() tale che
tale che
![]() .
Se X ha 0 elementi, allora
.
Se X ha 0 elementi, allora
![]() e
e
![]() .
Supponiamo che X abbia un solo elemento, ossia
.
Supponiamo che X abbia un solo elemento, ossia
![]() .
Dato che R è finito
.
Dato che R è finito
![]() è finito (e non vuoto
perché
è finito (e non vuoto
perché ![]() ), sia
), sia
![]() .
Consideriamo
.
Consideriamo
![]() il prodotto di tali
xi. Usando il lemma 22.8, si ha
il prodotto di tali
xi. Usando il lemma 22.8, si ha
![\begin{displaymath}\begin{array}[b]{rcrcrcrcr}
x_1\notin M \\
& \vcenter to 0...
... x_1\cdots x_s\notin M \\
& & & & & & x_s\notin M
\end{array}\end{displaymath}](img985.gif)
quindi
![]() .
D'altra parte se
.
D'altra parte se
![]() e
e ![]() allora
allora
![]() (altrimenti non sarebbe massimale) e quindi esiste i tale
che
(altrimenti non sarebbe massimale) e quindi esiste i tale
che ![]() .
Dato che N è un ideale,
.
Dato che N è un ideale,
![]() e
quindi
e
quindi
![]() .
Pertanto
.
Pertanto
![]() .
.
Supponiamo ora che X abbia n+1 elementi, allora possiamo scrivere
![]() con
con
![]() e Z costituito da un solo elemento. Allora Yha n elementi, per ipotesi di induzione esiste r tale che
e Z costituito da un solo elemento. Allora Yha n elementi, per ipotesi di induzione esiste r tale che
![]() e per
il caso n=1 esiste r' tale che
e per
il caso n=1 esiste r' tale che
![]() .
Ma allora
.
Ma allora
Sia X un insieme, allora la relazione di inclusione ![]() è un
ordinamento sull'insieme delle sue parti
è un
ordinamento sull'insieme delle sue parti
![]() .
.
La relazione ![]() è un ordinamento parziale sull'insieme
è un ordinamento parziale sull'insieme
![]() dei numeri naturali.
dei numeri naturali.
| a è massimo di X se: | |
| a è minimo di X se: | |
| a è maggiorante di Y se: | |
| a è minorante di Y se: | |
| a è estremo superiore di Y se: | a è minimo dei maggioranti di Y |
| (i.e. |
|
| a è estremo inferiore di Y se: | a è massimo dei minoranti di Y |
| (i.e. |
|
| a è massimale: |
|
| a è minimale: |
|
Dim. Diamo due dimostrazioni di questo fatto.
Prima dimostrazione. La relazione è riflessiva. Infatti se
![]() allora, poicé R è booleano, a=aa e quindi
allora, poicé R è booleano, a=aa e quindi ![]() .
.
La relazione è antisimmetrica. Se ![]() e
e ![]() allora, per definizione di
allora, per definizione di ![]() ,
a=ab e b=ba. Dato che R è
commutativo, ab=ba e quindi
a=b.
,
a=ab e b=ba. Dato che R è
commutativo, ab=ba e quindi
a=b.
La relazione è transitiva. Se ![]() e
e ![]() allora
a=ab e b=bc. Sostituiendo la seconda nella prima si ha allora che a=abced usando di nuovo la prima abc=ac e quindi a=ac, ossia
allora
a=ab e b=bc. Sostituiendo la seconda nella prima si ha allora che a=abced usando di nuovo la prima abc=ac e quindi a=ac, ossia ![]() .
.
Seconda dimostrazione. Sia
![]() il morfismo del teorema di
rappresentazione. Allora, dato che
il morfismo del teorema di
rappresentazione. Allora, dato che
![]() è iniettivo, si ha:
è iniettivo, si ha:
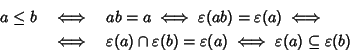
Nel seguito, quando parleremo di ordinamento di un anello booleano, ci riferiremo sempre a quello definito dalla precedente proprsizione.